Intake Theory
Helmholtz
Theory
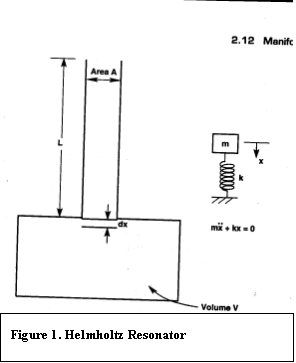
This theory refers to the modeling of the intake
runner and the cylinder volume as a spring-mass system, otherwise known as a
Helmholtz resonator. For simplicity, this theory refers to a system in which
the valve is wide open, and only refers to one of the runner-cylinder
combinations. The volume will act as a spring, since as more air is pushed into
the volume, the gas already present will compress. Hence, the pressure will
rise, and this will attempt to push the gases that are coming in, out. The air
being pushed into the volume can be modeled as a mass M, being pushed into a
volume V. The runner is of length L, with cross-sectional area A. The mass is
being pushed down a distance Δx. Hence, the mass being pushed into the
cylinder is
![]()
Following
this equation, ![]() is also the volume. Hence,
the equation becomes
is also the volume. Hence,
the equation becomes
![]()
which
signifies the increase in density. This increased density causes an increase in
pressure. This pressure change can be related to the speed of sound, since
pressure waves move at the speed of sound, assuming all changes are isentropic
and governed by
![]()
which,
by simplifying and taking derivatives, leads to
![]()
Also,
given that
![]()
the
force can be related to the isentropic speed of sound. Also, since the modeling
corresponds to the spring-mass system, and knowing that the force of a spring
is
![]()
hence,
![]()
Thus,
the “stiffness” of the air is directly related to the speed of sound. This
equation will be used in the solution of the spring-mass system. The equation
of motion, which governs this type of system, is given by
![]()
The
solution to this equation is given by the following,
![]()
The
resonant frequency, given by ω, has the solution
![]()
This equation can be related
to the speed of sound, by using the previously derived relationship, and
![]()
After plugging into the
frequency of the system, the following equation is obtained
![]()
This equation signifies that
the frequency of the pressure waves traveling through the intake manifold
branch is proportional to the speed of sound. The speed of sound is a molecular
property, which defines how the molecule will react to the application of
pressure. For our case, we are dealing with air, which can compress when
pressure is applied to it. Hence, analyzing
![]()
We can see that the speed of
sound is inversely proportional to the density of the medium. So in our case,
air is the medium, and the density of air increases as the mass of air is
pushed into the system. Hence, to keep the proportionality, the pressure must
increase. But for a solid, for instance, the density will not change for the
same amount of pressure applied to the air, hence another equation governs the
relationship between the solid and the speed of sound, which would have to be
much greater. This because the increase of pressure to the solid surface will
not change the density, hence the speed of sound will have to increase to keep
the proportionality.
Organ Pipe Theory
This is another theory used
to explain the behavior of pressure waves inside the intake branches. This
theory takes into account the compressibility of the flow. Hence, a
one-dimensional wave propagation theory can be used to explain this phenomenon.
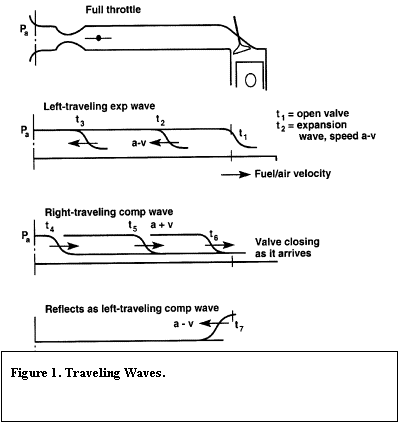
Two types of pressure waves
exist: compression waves and expansion waves. Compression waves result from an
increase in pressure, while expansion waves are due to a pressure drop.
Whenever any wave is
confronted by a change in area, two types of waves result: a transmitted wave and
a reflected wave. The transmitted waves are always of the same type as the
incident wave, be it a compression wave or expansion wave. The reflected wave
depends on the area it sees. If the incident wave sees a larger area, then the
reflected wave is of the other type. However, if the incident wave sees a
smaller area, the reflected wave is of the same type.
These definitions will be
useful for the following explanation regarding the pressure drops and increases
inside the runners. When the intake valve opens and the piston starts to drop,
the pressure in the cylinder becomes lower than that in the manifold. Hence,
since a drop in pressure produces an expansion wave, one of these results. This
wave travels through the inlet branch up until the junction where all the
branches begin. Hence, it sees a larger area. Thus, the reflected wave becomes
a compression wave. This compression wave travels down the manifold branch.
This compression wave should arrive at the valve right when the valve is
closing. This is because the compression wave will cause an increase in
pressure, and will help to fill the cylinder right before it closes. This
increases the volumetric efficiency of the engine. And since this compression
wave sees a smaller area, it is reflected as a compression wave. This all has
to be tuned very precisely, since these pressure waves are traveling at the
speed of sound.
This theory is formulated
assuming all other branches in the manifold are inactive, and the only active
branch is the one being considered.
Waves produced as a result
of the pressure differentials do go both waves, both into the cylinder and up
into the manifold branch. But the one that goes into the cylinder is disrupted
by the moving piston, hence has no consequence. Also, the waves that are
transmitted and go into the “inactive” branches are of no consequence, since
the valve will be closed when they arrive.
As for the exhaust, the same
principles apply. The only difference is the fact that a compression wave (not
an expansion wave) is produced when the valve opens (since there is an increase
in pressure). This wave travels down to the manifold branch, where it sees an
increase in area. Hence an expansion wave is reflected back towards the
cylinder. And since an expansion wave is associated with a pressure drop, it is
ideal that this wave arrives at the exhaust right when the valve is closing, to
help the cylinder get rid of the exhaust gases remaining. And again, only the
reflected waves are of interest.
Many of these waves interact
and produce many different effects on the system; hence an x-t diagram can be
produced. This then tracks the different waves as a function of the distance
they go and where they are relative to the manifold.
This discussion also goes
into the effect of the volumetric efficiency versus the RPM, both relating to
the manifold length. At any RPM, the pipe length will affect the volumetric
efficiency, since the waves will be traveling faster with higher RPM. Hence,
for faster traveling waves, a shorter pipe is needed for the tuning effects to
take place. However, lower RPMs produce slower moving waves, hence a shorter
pipe is needed to get the volumetric efficiency needed. This problem can be
addressed by folding the manifold. The manifold can be folded with an extra
valve, which may or may not allow the airflow through it, depending on the RPM.
This allows for maximum volumetric efficiency for different RPMs.