3.3 Example

From [1, p. 404, 30]

Asked: The area below $y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sin x^2$ for 0 $\raisebox{-.3pt}{$\leqslant$}$ $x$ $\raisebox{-.3pt}{$\leqslant$}$ 1.

3.3.1 Identification

$$\epsffile{approxx21.eps}$$

$$\int_0^1 \sin x^2 { \rm d}x$$

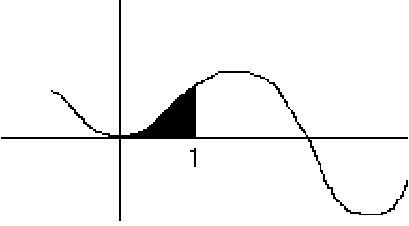
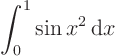
Analytically? Actually, the integral is equivalent to $\int(\sin(x)/x){ \rm d}x$, which cannot be written in terms of elementary functions.

But since the $x$ range is not large, we will try approximating $\sin x^2$ using a Taylor series.

3.3.2 Finish

The Taylor series of $\sin x^2$ is that of $\sin x$ with $x$ replaced by $x^2$. So:

$$\begin{array}{ll} \int_0^1 \sin x^2 { \rm d}x & \displa... ...{3!7} + \frac1{5!11} \\ & = .3103 \pm 0.0008 \end{array}$$

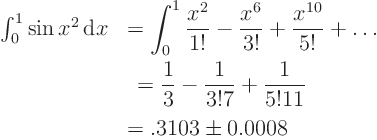
The error estimate is rigorous since the series is an alternating one whose terms get smaller monotoneously.