|
|
|
|
|
Next: 15.2 Diagonalization of nonsymmetric matrices |
|
![\begin{figure}
\centering
\setlength{\unitlength}{1pt}
\begin{picture}(...
...t(92.9,118.2){\makebox(0,0)[l]{$v_2'\vec p_2$}}
\end{picture}
\end{figure}](img465.gif) |
Normally, you use Cartesian coordinates
when dealing
with vectors. That is based on “Cartesian basis
vectors” ![]() . For example, in two
dimensions,
. For example, in two
dimensions,

components, or
coefficients,” or “coordinatesof vector
Therefore, in this way, you are never have to deal with more vectors
that ![]() and
and ![]() . All the rest is just ordinary numbers.
. All the rest is just ordinary numbers.
But sometimes it is convenient to use a different basis than the
obvious ![]() one. For example, you might know that in
dealing with plane stresses, it is often convenient to rotate the
coordinate system to the
one. For example, you might know that in
dealing with plane stresses, it is often convenient to rotate the
coordinate system to the principal axes.
In principal
axes, there are no shear stresses, just normal stresses. But if you
rotate the coordinate system, ![]() and
and ![]() become different
vectors, call them
become different
vectors, call them ![]() and
and ![]() . The point however is that
in using these new basis vectors
. The point however is that
in using these new basis vectors ![]() and
and ![]() , your
physical problem has simplified.
, your
physical problem has simplified.
As we will see later, to simplify a problem, the desired new vectors
are not always orthonormal (orthogonal and of length 1) like ![]() and
and ![]() in the example above. In general, the new basis vectors,
we will call them
in the example above. In general, the new basis vectors,
we will call them ![]() and
and ![]() , can be anything, as long
as they are linearly independent. As long as that is true, you can
still write any arbitrary vector
, can be anything, as long
as they are linearly independent. As long as that is true, you can
still write any arbitrary vector ![]() as
as
However, in general the coordinates ![]() and
and ![]() in the new basis
are not the same as the coordinates
in the new basis
are not the same as the coordinates ![]() and
and ![]() in the old basis
in the old basis
![]() . So, if you want to use the new basis to your
advantage, you will normally have to know how to compute
. So, if you want to use the new basis to your
advantage, you will normally have to know how to compute ![]() and
and
![]() if you know
if you know ![]() and
and ![]() and/or vice-versa. That is the
problem that this section will address.
and/or vice-versa. That is the
problem that this section will address.
First, to find the old coordinates ![]() and
and ![]() given the new ones
given the new ones
![]() and
and ![]() is easy. Just write the above equation as a
row-column multiplication:
is easy. Just write the above equation as a
row-column multiplication:
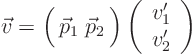
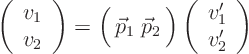
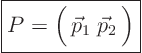 |
(15.1) |
So you get the following transformation formulae between coordinates
| (15.2) |
old to newreally means old from new.
The final thing you need to know is what happens to matrices. If a
matrix ![]() converts a vector
converts a vector ![]() to a vector
to a vector ![]() in terms of
Cartesian coordinates, then
in terms of
Cartesian coordinates, then ![]() should convert
should convert ![]() to
to
![]() in terms of the new coordinates. Since
in terms of the new coordinates. Since
So the transformation rules for matrices are
| (15.3) |
While we used a two dimensional example, you can do all of the above
in any number of dimensions. You just add more basis vectors to
transformation matrix ![]() .
.