| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
15.2 Diagonalization of nonsymmetric matrices
If a matrix 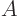 is not defective, you can use its eigenvectors as new
basis. It turns out that in that basis the matrix simplifies to a
diagonal matrix
is not defective, you can use its eigenvectors as new
basis. It turns out that in that basis the matrix simplifies to a
diagonal matrix
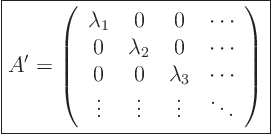 |
(15.4) |
Since this diagonal matrix has the eigenvalues on the main diagonal,
(in the order that you arranged the corresponding eigenvectors), it is
often written as 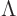 instead of
instead of 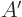 .
.
Needless to say, this simplification is a tremendous help if you are
doing analytical or numerical work involving the matrix.
The quickest was to see why 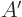 is diagonal like above is to note
that in terms of the new basis,
is diagonal like above is to note
that in terms of the new basis, 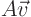 produces a new vector
produces a new vector
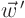 according to
according to
since 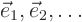 are eigenvectors of
are eigenvectors of 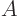 . So the
coefficients of
. So the
coefficients of 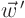 are related to those of
are related to those of 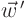 as
as 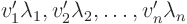 .
And that is just what multiplying by the diagonal matrix
.
And that is just what multiplying by the diagonal matrix 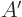 above
accomplishes.
above
accomplishes.
Recall from section 15.1 that the transformation
matrix 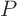 for change of basis to the eigenvectors must equal the
matrix
for change of basis to the eigenvectors must equal the
matrix 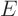 of eigenvectors. You therefore have for any vector
of eigenvectors. You therefore have for any vector 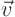 and matrix
and matrix 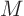 that you want to transform from new coordinates to
old or vice-versa:
that you want to transform from new coordinates to
old or vice-versa:
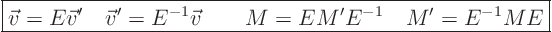 |
(15.5) |
Here the primes mean the vector or matrix as it appears in the new
basis of eigenvectors.
In summary, a nondefective matrix becomes diagonal when its
eigenvectors are used as basis. The main diagonal contains the
eigenvalues, ordered like the corresponding eigenvectors in 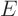 .
.
![]() is not defective, you can use its eigenvectors as new
basis. It turns out that in that basis the matrix simplifies to a
diagonal matrix
is not defective, you can use its eigenvectors as new
basis. It turns out that in that basis the matrix simplifies to a
diagonal matrix
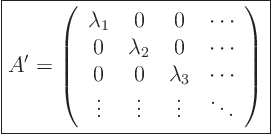
![]() is diagonal like above is to note
that in terms of the new basis,
is diagonal like above is to note
that in terms of the new basis, ![]() produces a new vector
produces a new vector
![]() according to
according to
![]() for change of basis to the eigenvectors must equal the
matrix
for change of basis to the eigenvectors must equal the
matrix ![]() of eigenvectors. You therefore have for any vector
of eigenvectors. You therefore have for any vector ![]() and matrix
and matrix ![]() that you want to transform from new coordinates to
old or vice-versa:
that you want to transform from new coordinates to
old or vice-versa:
![]() .
.