| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
15.3 Diagonalization of symmetric matrices
For symmetric matrices the same observations apply as for nonsymmetric
matrices in the previous section. But there are some further
considerations.
Most importantly, the eigenvectors, if found using the class
procedure, are orthonormal. So you can consider the eigenvectors
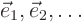 to be a rotated Cartesian basis.
To make this clearer to other people, you should rename
to be a rotated Cartesian basis.
To make this clearer to other people, you should rename 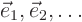 to
to 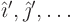 .
.
The most important other thing to remember is that the transformation
matrix
is now orthonormal. So be sure to use section 13.3 to
find its inverse.
Note further that if the determinant of the transformation matrix 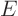 is negative, the rotated coordinate system is also left-handed instead
of right-handed. It corresponds to a mirroring of a coordinate
besides the rotation. If this bothers you, multiply one of the
eigenvectors by minus one.
is negative, the rotated coordinate system is also left-handed instead
of right-handed. It corresponds to a mirroring of a coordinate
besides the rotation. If this bothers you, multiply one of the
eigenvectors by minus one.
![]() to be a rotated Cartesian basis.
To make this clearer to other people, you should rename
to be a rotated Cartesian basis.
To make this clearer to other people, you should rename ![]() to
to ![]() .
.
![]() is negative, the rotated coordinate system is also left-handed instead
of right-handed. It corresponds to a mirroring of a coordinate
besides the rotation. If this bothers you, multiply one of the
eigenvectors by minus one.
is negative, the rotated coordinate system is also left-handed instead
of right-handed. It corresponds to a mirroring of a coordinate
besides the rotation. If this bothers you, multiply one of the
eigenvectors by minus one.