| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
16.2 Completing the square
Table 16.1:
Properties of the Laplace Transform.
(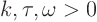 ,
, 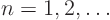 )
)
|
|
Completing the square simply means that you write a quadratic
as
If you multiply out, you see that it is the same.
One place where you often need this is in Laplace transforms. Laplace
transforms are often given in terms of a quadratic 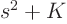 where
where 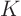 is an arbitrary constant. But you might have
is an arbitrary constant. But you might have 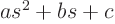 instead of
something of the form
instead of
something of the form 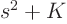 . However, you can write the part inside
the square brackets above as
. However, you can write the part inside
the square brackets above as 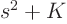 if you use the shift theorem to
account for the
if you use the shift theorem to
account for the 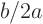 inside the parentheses. And the additional
factor
inside the parentheses. And the additional
factor 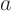 is trivial to account for.
is trivial to account for.
![\begin{displaymath}
a \bigg[
\bigg(
\underbrace{x+\frac{b}{2a}}_{\textstyl...
...rac{b^2}{4a^2}}_{\textstyle \rm {new\atop constant}}
\bigg]
\end{displaymath}](img559.gif)
![]() where
where ![]() is an arbitrary constant. But you might have
is an arbitrary constant. But you might have ![]() instead of
something of the form
instead of
something of the form ![]() . However, you can write the part inside
the square brackets above as
. However, you can write the part inside
the square brackets above as ![]() if you use the shift theorem to
account for the
if you use the shift theorem to
account for the ![]() inside the parentheses. And the additional
factor
inside the parentheses. And the additional
factor ![]() is trivial to account for.
is trivial to account for.