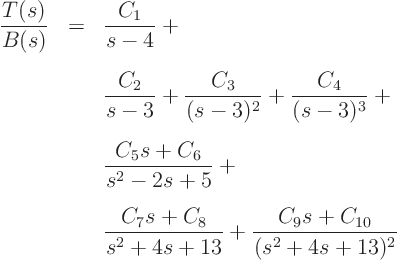| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
16.1 Partial Fractions
Partial fraction expansion simplifies fractions of the form
where 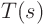 and
and 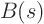 are polynomials in some variable
are polynomials in some variable 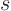 . This is
of importance, for example, in integration of such fractions and in
Laplace transformation. This section explains the procedure.
. This is
of importance, for example, in integration of such fractions and in
Laplace transformation. This section explains the procedure.
First, in case 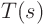 has a degree equal or higher than
has a degree equal or higher than 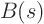 , you
should perform long division to take the ratio apart into powers of
, you
should perform long division to take the ratio apart into powers of
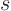 plus a remainder. That remainder is again a fraction of the form
plus a remainder. That remainder is again a fraction of the form
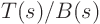 , but the new
, but the new 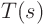 is of a degree less than
is of a degree less than 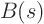 .
.
Now the only thing you still have to know is now how to deal with a
ratio 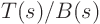 when the degree of
when the degree of 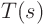 is less than that of
is less than that of
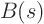 .
.
The first thing you will need to do is factor 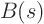 . Assume it is a
polynomial of some degree
. Assume it is a
polynomial of some degree 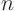 , in other words
, in other words
where 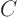 is some nonzero constant and the
is some nonzero constant and the 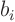 for
for
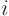

 are
are 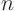 additional constants. You can simply
take
additional constants. You can simply
take 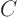 out of the entire ratio
out of the entire ratio 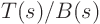 before proceeding. From
now on, it will be assumed that you have done that, so that there is
no longer a
before proceeding. From
now on, it will be assumed that you have done that, so that there is
no longer a 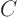 in the above expression to worry about. It is then
known from complex variable theory that
in the above expression to worry about. It is then
known from complex variable theory that 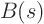 can always be written
in the form
can always be written
in the form
Here the 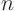 constants
constants 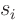 , (
, (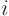

 ), are the
locations, or roots, where
), are the
locations, or roots, where 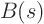 is zero. So
is zero. So 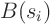
 0 for
0 for
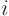

 . Note that some of these roots may coincide.
In other words some of the
. Note that some of these roots may coincide.
In other words some of the 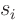 may be equal to each other. For
example
may be equal to each other. For
example
has 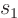

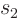
 1 and
1 and 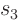

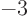 .
.
There is a further complication. Some of the roots 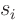 may be
complex. For example, a quadratic with a negative discriminant has
complex roots instead of real ones. However, assuming that the
polynomial
may be
complex. For example, a quadratic with a negative discriminant has
complex roots instead of real ones. However, assuming that the
polynomial 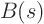 is real, (for real
is real, (for real 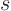 ), you would probably not want
to deal with complex numbers. You can avoid that because for real
), you would probably not want
to deal with complex numbers. You can avoid that because for real
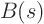 , the complex roots come in “complex-conjugate
pairs.” That means that for every complex root
, the complex roots come in “complex-conjugate
pairs.” That means that for every complex root 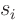 there is a
second root
there is a
second root 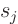 so that
so that 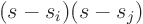 is a real quadratic
with roots
is a real quadratic
with roots 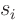 and
and 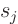 . So a real
. So a real 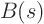 can always be written as
a product of real factors linear in s and real factors quadratic in s.
can always be written as
a product of real factors linear in s and real factors quadratic in s.
For example, you might have a 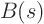 that can be written as
that can be written as
That would be a polynomial of degree 10, (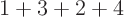
 10). For this
10). For this
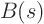 , any desired ratio
, any desired ratio 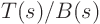 can be written as
can be written as
The right hand side is the partial fraction expansion of the ratio.
Note that the individual terms in the partial fraction expansion are
much simpler than the original ratio. The original ratio has a
polynomial of degree 10 in the bottom. And a polynomial of a degree
up to 9 in the top. So if you want to do anything with the given
ratio, it will become much easier if you use the right hand side above
to do it. That is why you want to do partial fraction expansions.
That leaves two key questions to be answered:
- In general, how do you know what terms there are in the right
hand side?
- How do you find the values of all these coefficients
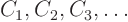 ?
?
The answer to the first question is as follows;
- For every factor
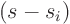 that appears
that appears 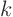 times in
times in
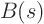 , there are terms in the right hand side of the form
, there are terms in the right hand side of the form
Check it out for the factors 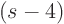 (single) and
(single) and 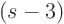 (triple)
in the example given earlier. (What you want to call the constants
is of course up to you, as long as each has a unique name.)
(triple)
in the example given earlier. (What you want to call the constants
is of course up to you, as long as each has a unique name.)
- For every factor
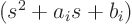 that appears
that appears 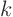 times in
times in
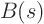 , there are terms in the right hand side of the form
, there are terms in the right hand side of the form
Check it out for the factors 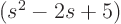 (single) and
(single) and 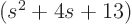 (double) in the example above.
(double) in the example above.
The second question was how to find all these constants. The method
you must use in this class is to crunch it out:
- Bring all the terms in the partial fraction expansion over
the common denominator
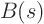 .
.
- Multiply out the top. This must equal the given
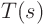 . So the
net coefficient of each power of
. So the
net coefficient of each power of 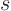 must match the corresponding
coefficient in
must match the corresponding
coefficient in 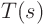 . That gives you your equations for your
unknown coefficients. Use Gaussian elimination to solve them.
. That gives you your equations for your
unknown coefficients. Use Gaussian elimination to solve them.
For the example, its partial fraction expansion becomes, when brough
over the common denominator 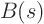 :
:
Multiply out the top, (don't make any mistakes, of course), then
equate the net coefficients of the 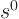 ,
, 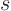 ,
, 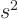 , ...,
, ..., 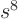 and
and 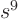 powers to the corresponding coefficients in the given
powers to the corresponding coefficients in the given 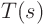 .
That gives 10 equations for the 10 unknowns
.
That gives 10 equations for the 10 unknowns 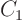 ,
, 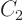 , ...
, ...
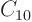 . Solve using Gaussian elimination. (Cramer's rule is
not recommended.) That will be fun!
. Solve using Gaussian elimination. (Cramer's rule is
not recommended.) That will be fun!
Note: Of course, if 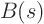 is not real, there is no point in using
quadratics. Just expand in linear factors of the form
is not real, there is no point in using
quadratics. Just expand in linear factors of the form 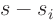 (with
(with
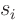 now complex) only.
now complex) only.
Note: there are more intelligent ways of finding the coefficients than
crunching it out as we must do in this class. For example, consider
once more the example:
If you multiply the expansion in the right hand side by the single
factor 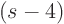 and then evaluate it at
and then evaluate it at 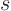
 4, you get
4, you get 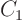 . (All the
other terms are zero at
. (All the
other terms are zero at 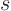
 4 because of the multiplication by
4 because of the multiplication by
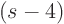 .) The bottom line is therefore that if you multiply the
left hand side by
.) The bottom line is therefore that if you multiply the
left hand side by 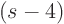 and then evaluate it at
and then evaluate it at 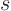
 4, you
get
4, you
get 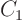 too. And that is doable because the left hand side is
given. (To evaluate at
too. And that is doable because the left hand side is
given. (To evaluate at 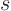
 4, you either need to divide out the
common factor
4, you either need to divide out the
common factor 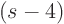 from top and bottom or use l’Hopital once.
Dividing out the common factor from top and bottom is a simple matter
of a long division of the bottom if you have it in unfactored form.)
To find
from top and bottom or use l’Hopital once.
Dividing out the common factor from top and bottom is a simple matter
of a long division of the bottom if you have it in unfactored form.)
To find 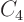 , multiply by
, multiply by 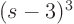 and evaluate at
and evaluate at 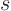
 3. To find
3. To find
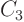 , multiply by
, multiply by 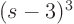 , differentiate the result once, and
evaluate at
, differentiate the result once, and
evaluate at 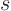
 3. Etcetera. Especially if you want just a single
coefficient, this can be much more convenient. Or you can use it
to test the correctness of a few sample coefficients.
3. Etcetera. Especially if you want just a single
coefficient, this can be much more convenient. Or you can use it
to test the correctness of a few sample coefficients.
![]() has a degree equal or higher than
has a degree equal or higher than ![]() , you
should perform long division to take the ratio apart into powers of
, you
should perform long division to take the ratio apart into powers of
![]() plus a remainder. That remainder is again a fraction of the form
plus a remainder. That remainder is again a fraction of the form
![]() , but the new
, but the new ![]() is of a degree less than
is of a degree less than ![]() .
.
![]() when the degree of
when the degree of ![]() is less than that of
is less than that of
![]() .
.
![]() . Assume it is a
polynomial of some degree
. Assume it is a
polynomial of some degree ![]() , in other words
, in other words
![]() may be
complex. For example, a quadratic with a negative discriminant has
complex roots instead of real ones. However, assuming that the
polynomial
may be
complex. For example, a quadratic with a negative discriminant has
complex roots instead of real ones. However, assuming that the
polynomial ![]() is real, (for real
is real, (for real ![]() ), you would probably not want
to deal with complex numbers. You can avoid that because for real
), you would probably not want
to deal with complex numbers. You can avoid that because for real
![]() , the complex roots come in “complex-conjugate
pairs.” That means that for every complex root
, the complex roots come in “complex-conjugate
pairs.” That means that for every complex root ![]() there is a
second root
there is a
second root ![]() so that
so that ![]() is a real quadratic
with roots
is a real quadratic
with roots ![]() and
and ![]() . So a real
. So a real ![]() can always be written as
a product of real factors linear in s and real factors quadratic in s.
can always be written as
a product of real factors linear in s and real factors quadratic in s.
![]() that can be written as
that can be written as
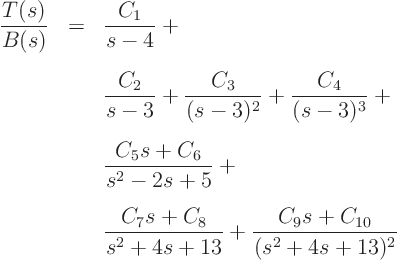
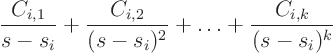
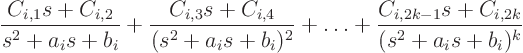
![]() :
:
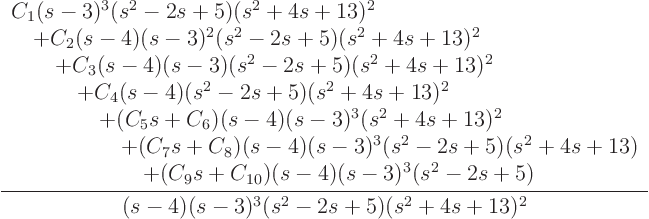
![]() is not real, there is no point in using
quadratics. Just expand in linear factors of the form
is not real, there is no point in using
quadratics. Just expand in linear factors of the form ![]() (with
(with
![]() now complex) only.
now complex) only.