| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
14.1 Finding Eigenvalues
In this class, to find the eigenvalues of an 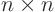 matrix,
matrix,
-
1.
- Form the matrix
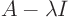 . That means, add
. That means, add 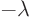 to
each diagonal elements. (Don't forget zero diagonal elements.)
to
each diagonal elements. (Don't forget zero diagonal elements.)
-
2.
- Find the determinant of that matrix using the method of
minors. (Gaussian elimination is too messy here and should not
be used.)
-
3.
- Set this determinant to zero. For an
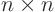 matrix,
the determinant can always be written in the form
matrix,
the determinant can always be written in the form
where 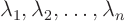 are the
eigenvalues. They are found as the roots (or zeros) of the
determinant. There are always
are the
eigenvalues. They are found as the roots (or zeros) of the
determinant. There are always 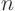 eigenvalues. But these
eigenvalues. But these 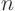 eigenvalues do not necessarily correspond to
eigenvalues do not necessarily correspond to 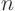 different numbers.
For example, for some matrix
different numbers.
For example, for some matrix 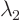 might be the same number as
might be the same number as
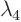 . In that case, that number is called a “double
eigenvalue”. If three of the eigenvalues are the same
number, that number is called a
. In that case, that number is called a “double
eigenvalue”. If three of the eigenvalues are the same
number, that number is called a triple eigenvalue,
etcetera.
For an 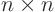 matrix, the determinant is always a polynomial of
degree
matrix, the determinant is always a polynomial of
degree 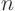 , call it
, call it 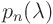 . Now finding the roots of
quadratics,
. Now finding the roots of
quadratics, 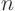
 2, is easy. But if the dimension of the matrix
2, is easy. But if the dimension of the matrix
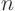
 3, you have to solve a cubic equation. For that the general
solution is very and hard to apply, especially if you do not know
complex variables. For
3, you have to solve a cubic equation. For that the general
solution is very and hard to apply, especially if you do not know
complex variables. For 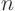
 4, the general solution is even
worse, and for
4, the general solution is even
worse, and for 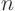
 5 or more, there is no general expression for
the roots at all. (It has in fact been proved that such an expression
is impossible to find.) To deal with such problems, here are some
tricks:
5 or more, there is no general expression for
the roots at all. (It has in fact been proved that such an expression
is impossible to find.) To deal with such problems, here are some
tricks:
- Do not be too quick to multiply out. Maybe you can recognize a
common factor
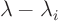 in all terms before multiplying
out. In that case,
in all terms before multiplying
out. In that case, 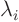 is one of your eigenvalues. To find
the remaining eigenvalues, take the factor
is one of your eigenvalues. To find
the remaining eigenvalues, take the factor 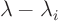 out
of the entire expression and look at what is left.
out
of the entire expression and look at what is left.
- If you can guess a root
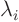 (by trying, say, 0,
(by trying, say, 0, 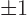 ,
,
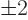 , ..., and seeing whether the determinant is zero for that
value of
, ..., and seeing whether the determinant is zero for that
value of 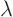 ), then you can write the original characteristic
polynomial
), then you can write the original characteristic
polynomial 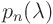 as
as 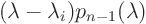 where
where 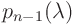 is one degree less that
is one degree less that 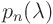 . So
its roots are easier to find. You find
. So
its roots are easier to find. You find 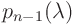 by long
division of
by long
division of 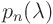 by
by 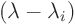 .
.
- Sometimes a fourth order polynomial is really just a quadratic
when written in terms of
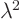 , like
, like
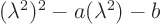 . In that case, first find the values
of
. In that case, first find the values
of 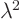 , then from those the values of
, then from those the values of 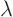 .
.
![]() matrix,
matrix,
![]() matrix, the determinant is always a polynomial of
degree
matrix, the determinant is always a polynomial of
degree ![]() , call it
, call it ![]() . Now finding the roots of
quadratics,
. Now finding the roots of
quadratics, ![]()
![]() 2, is easy. But if the dimension of the matrix
2, is easy. But if the dimension of the matrix
![]()
![]() 3, you have to solve a cubic equation. For that the general
solution is very and hard to apply, especially if you do not know
complex variables. For
3, you have to solve a cubic equation. For that the general
solution is very and hard to apply, especially if you do not know
complex variables. For ![]()
![]() 4, the general solution is even
worse, and for
4, the general solution is even
worse, and for ![]()
![]() 5 or more, there is no general expression for
the roots at all. (It has in fact been proved that such an expression
is impossible to find.) To deal with such problems, here are some
tricks:
5 or more, there is no general expression for
the roots at all. (It has in fact been proved that such an expression
is impossible to find.) To deal with such problems, here are some
tricks: