| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
14.2 Eigenvectors of nonsymmetric matrices
To find the eigenvectors of a nonsymmetric matrix,
-
1.
- Find the eigenvalues of the matrix as described.
-
2.
- For each distinct eigenvalue
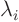 , find the basis
of the null space of
, find the basis
of the null space of 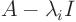 . This basis forms a complete
set of eigenvectors
. This basis forms a complete
set of eigenvectors 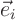 for the eigenvalue.
The method for finding nullspaces was discussed earlier.
for the eigenvalue.
The method for finding nullspaces was discussed earlier.
There is always at least one eigenvector. However, for a multiple
eigenvalue, the number of eigenvectors might be less than the
multiplicity of the eigenvalue. If so, the matrix is
defective. (This is not to be confused with singular. A
matrix is singular if an eigenvalue is zero, making its determinant
zero.) For example, a matrix is defective if a double eigenvalue has
only one eigenvector. Or a triple eigenvector only one or two.