| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
4.1 Introduction
Taylor series often do not work because the functions involved are
not analytic at the point of interest. For example, this is common
if the behavior of interest is at large time, or for large values
of some other parameter, like the Reynolds number Re of a flow.
(In fact, for flows in infinite domains it normally also occurs
for small Reynolds numbers.
Finding nonanalytic limits is then needed. Applications are very
similar to those of Taylor series:
- Because it is needed.
- To reduce effort.
- To increase accuracy.
- For making estimates of how importants something is.
- To get more insight. For example, consider the laminar flow
past a flat plate if the plate is aligned with the incoming flow
velocity
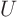 . For finite Reynolds numbers, there is little more you
can say than that the flow velocity will be zero at the plate, and
. For finite Reynolds numbers, there is little more you
can say than that the flow velocity will be zero at the plate, and
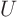 far away from the plate. To get more insight than that, you can
ask: “What is the limit of the velocity for infinite Reynolds
number Re, assuming that you keep the streamwise location
far away from the plate. To get more insight than that, you can
ask: “What is the limit of the velocity for infinite Reynolds
number Re, assuming that you keep the streamwise location 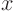 fixed,
as well as keep the ratio
fixed,
as well as keep the ratio 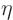

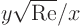 fixed, where
fixed, where 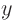 the distance from the wall?” The answer is
the distance from the wall?” The answer is 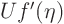 where
where
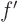 is the Blasius function tabulated in any real book on fluid
mechanics. (If you instead keep
is the Blasius function tabulated in any real book on fluid
mechanics. (If you instead keep 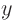 itself fixed at a nonzero
value, the limit is
itself fixed at a nonzero
value, the limit is 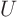 , which is not very interesting.) Most of my
theoretical research in fluids (as opposed to in numerical methods)
really simply finds limits like this.
, which is not very interesting.) Most of my
theoretical research in fluids (as opposed to in numerical methods)
really simply finds limits like this.
- ...