4.2 Example

From [1, p. 227, 10v]

Asked:

$$\lim_{x\to - \infty} x^2 e^x$$

4.2.1 Observations

$$\lim_{x\to - \infty} x^2 e^x$$

You must first look whether the limit is trivial:

$$x^2 \to \infty \qquad e^x \to 0$$

Since the product of infinity times zero is unknown, this limit is nontrivial.

4.2.2 L'Hopital

L'Hopital can be used if you create a ratio of quantities that both become zero or both become infinite. (For example, you would not want to apply L'Hopital on $\lim_{x\to0}3/2$.)

$$\lim_{x\to - \infty} \frac{x^2}{e^{-x}} = \lim_{x\to - \infty} \frac{\left(x^2\right)'}{\left(e^{-x}\right)'}$$

Now both top and bottom become infinite. So L'Hopital can be applied, by differentiating top and bottom separately:

$$\lim_{x\to - \infty} \frac{\left(x^2\right)'}{\left(e^{-x}\right)'} = \lim_{x\to - \infty} \frac{2x}{-e^{-x}} =$$

Still infinity over infinity, so differentiate once more

$$\lim_{x\to - \infty} \frac{2x}{-e^{-x}} = \lim_{x\to - \infty} \frac{2}{e^{-x}} = 0$$

4.2.3 Better

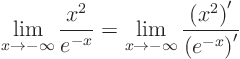
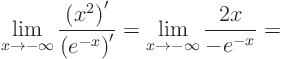
Using some insight is always better than just crunching it out. First simplify things for yourself by defining $u$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-x$. Then $u$ goes to plus infinity instead of minus infinity like $x$. Then

$$\lim_{x\to-\infty} x^2 e^x \lim_{u\to\infty} \frac{u^2}{e^{u}}$$

and that is zero because $e^u$ is much greater than any power of $u$ for large positive $u$. (To see that, just look at the Taylor series:

$$e^u = 1 + \frac{u}{1!} + \frac{u^2}{2!} + \frac{u^3}{3!} + \ldots$$

The $u^3$ term is much larger than $u^2$ for large $u$ and the other terms make $e^u$ larger still.)

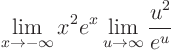
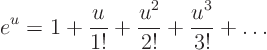
So you could replace $x^2$ by $x^{100}$ and the limit would still be zero.