4.3 Example

From [1, p. 228, 10z]

Asked:

$$\lim_{x\to 0} (x - \arcsin x) \csc^3 x$$

4.3.1 Grinding it out

In

$$\lim_{x\to 0} (x - \arcsin x) \csc^3 x$$

$x$ and $\arcsin x$ become zero, but $\csc x$ becomes infinite. The total is undefined.

The simplest way to make a ratio suitable for l’Hopital is to use that $\csc x \equiv 1/\sin x$:

$$\lim_{x\to 0} (x - \arcsin x) \csc^3 x = \lim_{x\to 0} \frac{x - \arcsin x}{\sin^3 x}$$

Differentiate top and bottom

$$\lim_{x\to 0} \frac{1 - (1-x^2)^{-1/2}}{3 \sin^2 x \cos x}$$

Still zero over zero, so differentiate again

$$\lim_{x\to 0} \frac{ - x (1-x^2)^{-3/2}}{6 \sin x \cos^2 x -3 \sin^3 x}$$

Still zero over zero, so differentiate again

$$\lim_{x\to 0} \frac{ - (1-x^2)^{-3/2} - 3 x^2 (1-x^2)^{-3/... ... {6 \cos^3 x - 21 \sin^2 x \cos x} = {\textstyle\frac{1}{6}}$$

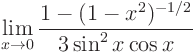
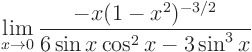
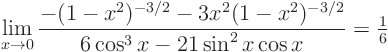
If I did not make any mistakes, I guess.

4.3.2 Using insight

Since $\sin x \approx x$ for small $x$, $\sin^3 x \approx x^3$. Also looking at a mathematical handbook, $\arcsin x \approx x + \frac16 x^3 + \ldots$. So:

$$\lim_{x\to 0} \frac{x - \arcsin x}{\sin^3 x} \approx \frac{-\frac16 x^3}{x^3} = - {\textstyle\frac16}$$

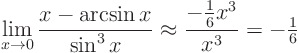
(Note that we needed to keep the cubic term in the Taylor series for $\arcsin x$ since the term $x$ dropped out.)