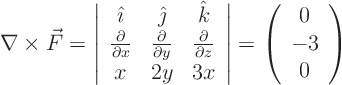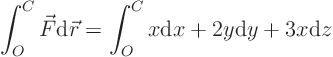7.2 Example

From [1, p. 487, 14e]

Given: $\vec F = x {\hat\imath}+ 2y {\hat\jmath}+ 3x {\hat k}$

$$\hbox{\epsffile{linint.eps}}$$

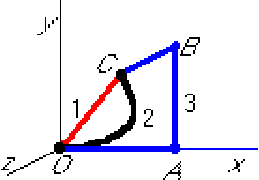
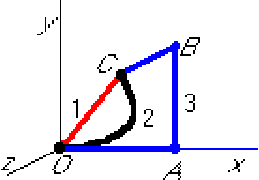
Asked: The work done by this force going from O to C along (1) the connecting line; (2) the curve $x=t$, $y=t^2$, $z=t^3$; (3) path OABC.

7.2.1 Identification

Find the curl of the vector to see whether the three integrals are going to be the same:

$$\nabla \times \vec F = \left\vert \begin{array}{ccc} {... ... = \left( \begin{array}{c} 0 -3 0 \end{array} \right)$$

Nonzero, so the integrals along the three paths need not be the same.

7.2.2 Solution

$$\int_O^C \vec F {\rm d}\vec r = \int_O^C x {\rm d}x + 2 y {\rm d}y + 3 x {\rm d}z$$

$$\epsffile{linint.eps}$$

1. Along the line $y=x$ and $z=x$:
   
   $$\int_{x=0}^1 6x {\rm d}x = 3$$
   
   

2. Along the curve $x=t$, $y=t^2$, $z=t^3$:
   
   $$\int_{t=0}^1 F_x \frac{{\rm d}x}{{\rm d}t} + F_y \frac{{\r... ...}t + 2t^2 2t {\rm d}t + 3 t 3t^2 {\rm d}t = \frac{15}4$$
   
   

3. Along OABC:
   
   $$\int_{x=0}^1 x {\rm d}x + \int_{y=0}^1 2 y {\rm d}y + \int_{z=0}^1 3 1 {\rm d}z = \frac 92$$