6.2 Example

From [1, p. 338, 14]

Given: A particle moves along a curve described by

$$x = {\textstyle\frac{1}{2}} t^2 \qquad y = {\textstyle\frac{1}{2}} x^2 - {\textstyle\frac{1}{4}} \ln x$$ (6.1)

Asked: The velocity and acceleration at $t=1$

$$\epsffile{motion1.eps}$$

6.2.1 Position

At $t=1$:

$$x = {\textstyle\frac{1}{2}} t^2 = {\textstyle\frac{1}{2}} ... ...style\frac{1}{2}} x^2 - {\textstyle\frac{1}{4}} \ln x = 0.298$$ (6.2)

hence

$$\vec r = \left(\begin{array}{c} 0.5 0.298 \end{array}\right) = 0.5 {\hat\imath}+ 0.298 {\hat\jmath}$$ (6.3)

6.2.2 Velocity

Velocity:

$$\vec v = \left( \begin{array}{c} \displaystyle \frac... ...} t \frac12 t^3 - \frac12 t^{-1} \end{array} \right)$$ (6.4)

Velocity at $t=1$:

$$\vec v(1) = \left( \begin{array}{c} 1 0 \end{array} \right) = 1 {\hat\imath}+ 0 {\hat\jmath}= {\hat\imath}$$ (6.5)

Components at $t=1$:

$$v_x \equiv \frac{{\rm d}x}{{\rm d}t} = 1 \qquad v_y \equiv \frac{{\rm d}y}{{\rm d}t} = 0$$ (6.6)

$$\epsffile{motion2.eps}$$

Magnitude at $t=1$:

$$\vert\vec v\vert = v \equiv \frac{{\rm d}s}{{\rm d}t} = \sqrt{v_x^2 + v_y^2} = 1$$ (6.7)

Angle with the positive $x$-axis at $t=1$:

$$\tau = \arctan \frac{v_y}{v_x} = 0 \mbox{ (not $\pi$)}.$$ (6.8)

6.2.3 Acceleration

Acceleration:

$$\vec a = \left( \begin{array}{c} \displaystyle \frac... ...} 1 \frac32 t^2 + \frac12 t^{-2} \end{array} \right)$$ (6.9)

from (6.4).

Acceleration at $t=1$:

$$\vec a(1) = \left( \begin{array}{c} 1 2 \end{array} \right) = 1 {\hat\imath}+ 2 {\hat\jmath}$$ (6.10)

Components at $t=1$:

$$a_x \equiv \frac{{\rm d}v_x}{{\rm d}t} = 1 \qquad a_y \equiv \frac{{\rm d}v_y}{{\rm d}t} = 2$$ (6.11)

$$\epsffile{motion3.eps}$$

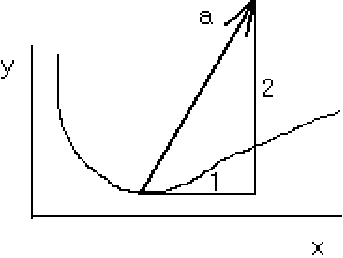
Magnitude at $t=1$:

$$\vert\vec a\vert = a = \sqrt{a_x^2 + a_y^2} = \sqrt{5}$$ (6.12)

Angle with the positive $x$-axis at $t=1$:

$$\phi = \arctan \frac{a_y}{a_x} = 63^\circ \mbox{ (not $243^\circ$)}.$$ (6.13)

Component tangential to the motion:

$$a_t \equiv \frac{{\rm d}v}{{\rm d}t} \equiv \frac{{\rm d}^... ...ec v\vert} = \frac{a_x v_x + a_y v_y}{\vert\vec v\vert} = 1$$ (6.14)

Component normal to the motion:

$$a_n \equiv \frac{v^2}{R} = \sqrt{a^2 - a_t^2} = 2$$ (6.15)