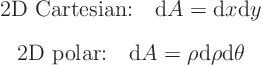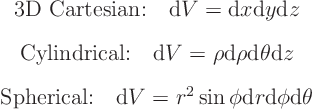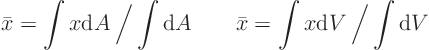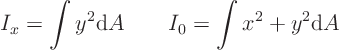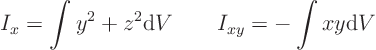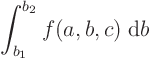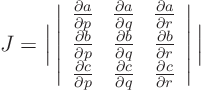| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
8.1 Introduction
Multiple integrals are used to find various engineering quantities:
- Areas (cost, heat losses, ...):
- Volumes (weight, ...):
- Centroids (center of gravity, center of pressure, ...)
- Moments of inertia (solid body dynamics, center of pressure, ...)
- ...
If the material is not homogenous, you may have to put an additional
density-like factor in those integrals.
Procedure:
- Draw the region to be integrated over.
- When integrating, say
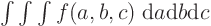 ,
you have to decide whether you want to do
,
you have to decide whether you want to do 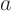 ,
, 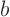 , or
, or 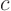 first.
Usually, you do the coordinate with the easiest limits of
integration first.
first.
Usually, you do the coordinate with the easiest limits of
integration first.
- If you decide to do, say,
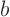 first, (i.e. you want to integrate
first, (i.e. you want to integrate
first), the limits of integration 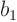 and
and 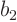 must be identified
from the graph at arbitrary
must be identified
from the graph at arbitrary 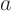 and
and 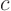 , and are normally
functions of
, and are normally
functions of 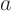 and
and 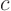 :
: 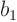

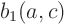 ,
, 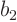

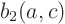 .
.
- After integrating over, say,
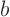 , the remaining double integral
should no longer depend on
, the remaining double integral
should no longer depend on 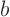 in any way. Nor does the region of
integration: redraw it without the
in any way. Nor does the region of
integration: redraw it without the 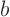 coordinate. In other words,
project it onto the
coordinate. In other words,
project it onto the 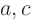 -plane. Then integrate over the next
easiest coordinate in the same way.
-plane. Then integrate over the next
easiest coordinate in the same way.
- If you change integration variables from
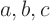 to
to 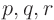 ,
the integral becomes
,
the integral becomes 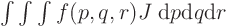 with the
with the Jacobian
Here the inner bars indicate the determinant of the matrix of
derivatives and the outer bars the absolute value of that.
(Sometimes it is easier to take the inverse of the Jacobian of the
inverse transformation.)