8.2 Example

From [1, p. 487, 14e]

Asked: Find the centroid of the first-quadrant area bounded by $x^2-8y+4$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 and $x^2$ $\vphantom0\raisebox{1.5pt}{$=$}$ $4y$ and $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0.

8.2.1 Region

$$\hbox{\epsffile{mulintx11.eps}}$$

8.2.2 Approach

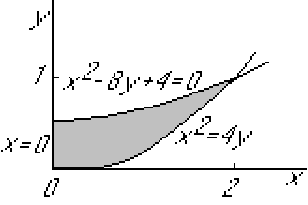
Integrate $x$ first?

$$\hbox{\epsffile{mulintx12.eps}}$$

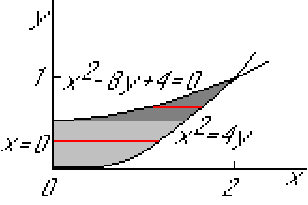
The integral would have to be split up into the light and dark areas since the lower boundary of integration is $x_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 in the light region and $x_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\sqrt{8y-4}$ in the dark region.

So integrate $y$ first!

$$\hbox{\epsffile{mulintx13.eps}}$$

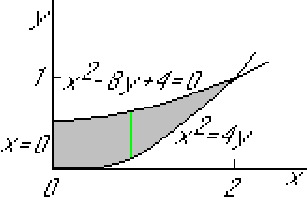
The boundaries of integration will be

$$y_1 = {\textstyle\frac{1}{4}} x^2 \qquad y_2 = {\textstyle\frac{1}{8}} x^2 + {\textstyle\frac{1}{2}}$$

After integration over $y$, the remaining region of integration over $x$ will be a line segment:

$$\hbox{\epsffile{mulintx14.eps}}$$

$$x_1 = 0 \qquad x_2 = 2$$

8.2.3 Results

$$\hbox{\epsffile{mulintx13.eps}}$$

For $A$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int{\rm d}A$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int\int{\rm d}x{\rm d}y$:

$$A = \int_{x=0}^{x=2} \left[\int_{y=\frac14 x^2}^{y=\frac18x^2+\frac12}\; {\rm d}y\right]\; {\rm d}x$$

$$= \int_{x=0}^{2} \left[ y \Big\vert _{y=\frac14 x^2}^{y=\frac18x^2+\frac12}\right]\; {\rm d}x$$

$$= \int_{x=0}^{2} \left[ ({\textstyle\frac{1}{8}}x^2+{\text... ...\frac{1}{2}}) - ({\textstyle\frac{1}{4}} x^2)\right] {\rm d}x$$

$$= \int_{x=0}^{2} \left[ ({\textstyle\frac{1}{2}} - {\textstyle\frac{1}{8}} x^2\right] {\rm d}x = {\textstyle\frac{2}{3}}$$

$$\hbox{\epsffile{mulintx13.eps}}$$

For $A\bar x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int x{\rm d}A$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int\int x{\rm d}x{\rm d}y$:

$$A = \int_{x=0}^{x=2} \left[\int_{y=\frac14 x^2}^{y=\frac18x^2+\frac12} x\; {\rm d}y\right]\; {\rm d}x$$

where $x$ is constant in the integration;

$$= \int_{x=0}^{2} \left[ x y \Big\vert _{y=\frac14 x^2}^{y=\frac18x^2+\frac12}\right]\; {\rm d}x$$

$$= \int_{x=0}^{2} \left[ ({\textstyle\frac{1}{8}}x^3+{\text... ...frac{1}{2}}x) - ({\textstyle\frac{1}{4}} x^3)\right] {\rm d}x$$

$$= \int_{x=0}^{2} \left[ ({\textstyle\frac{1}{2}}x - {\text... ...e\frac{1}{8}} x^3\right] {\rm d}x = {\textstyle\frac{1}{2}}$$

Hence $\bar x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac12/\frac23$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac34$.

For $A\bar y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int y {\rm d}A$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\int\int y {\rm d}x {\rm d}y$:

$$A = \int_{x=0}^{x=2} \left[\int_{y=\frac14 x^2}^{y=\frac18x^2+\frac12} y\; {\rm d}y\right]\; {\rm d}x$$

$$= \int_{x=0}^{2} \left[ {\textstyle\frac{1}{2}} y^2 \B... ...ert _{y=\frac14 x^2}^{y=\frac18x^2+\frac12}\right]\; {\rm d}x$$

$$= \int_{x=0}^{2} \left[ {\textstyle\frac{1}{2}}({\textst... ...le\frac{1}{2}}({\textstyle\frac{1}{4}} x^2)^2\right] {\rm d}x$$

$$= \int_{x=0}^{2} \left[ ({\textstyle\frac{1}{8}} + {\texts... ...rac{3}{128}} x^2\right] {\rm d}x = {\textstyle\frac{4}{15}}$$

Hence $\bar y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac4{15}/\frac23$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac25$.