|
|
|
|
|
Next: 9. Numerical Integration |
|
From [1, p. 507, 21c]
Asked: Find the centroid of the first octant region
inside ![]()
![]() 9 and below
9 and below ![]()
![]() 4.
4.
The region inside ![]()
![]() 9 is the inside of a cylinder of radius 3
around the z-axis. The equation
9 is the inside of a cylinder of radius 3
around the z-axis. The equation ![]()
![]() 4 describes a plane through the
4 describes a plane through the
![]() -axis under 45 degrees with the
-axis under 45 degrees with the ![]() -axis:
-axis:
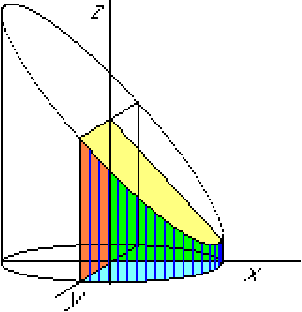
Use cylindrical coordinates ![]() ,
, ![]() , and
, and ![]() :
:
Integrate ![]() first:
first:
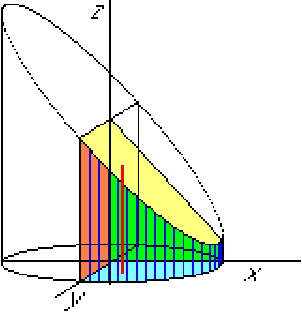
(Why not ![]() first? Why not
first? Why not ![]() ?).
Boundaries are
?).
Boundaries are
Next integrate ![]() and
and ![]() :
:

For the volume ![]()
![]()
![]()
![]()
![]() :
:
![\begin{displaymath}
V = \int_{\theta=0}^{\pi/2}
\int_{r=0}^{3}
\left[
\i...
...cos\theta} r \; {\rm d}z
\right]
{\rm d}r
{\rm d}\theta
\end{displaymath}](img288.gif)
![\begin{displaymath}
= \int_{\theta=0}^{\pi/2}
\left[
\int_{r=0}^{3}
(4-r\cos\theta) r
{\rm d}r
\right]
{\rm d}\theta
\end{displaymath}](img289.gif)
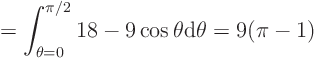
For ![]()
![]()
![]()
![]()
![]() :
:
![\begin{displaymath}
V \bar x = \int_{\theta=0}^{\pi/2}
\int_{r=0}^{3}
\lef...
... \cos \theta \; {\rm d}z
\right]
{\rm d}r
{\rm d}\theta
\end{displaymath}](img294.gif)
![\begin{displaymath}
= \int_{\theta=0}^{\pi/2}
\left[
\int_{r=0}^{3}
4r^2\cos\theta -r^3\cos^2\theta
{\rm d}r
\right]
{\rm d}\theta
\end{displaymath}](img295.gif)
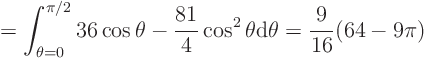
Etcetera.