9.1 Introduction

$$\epsffile{numinti1.eps}$$

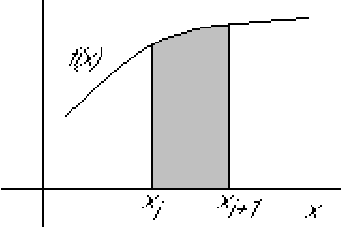
Numerical integration using Newton formulae:

• can handle any function;
• simple;
• can handle measured data easily.

Trapezium rule for an interval from $x=x_i$ to $x_{i+1}$:

$$\int_{x_i}^{x_{i+1}} f(x)\; {\rm d}x \approx \left(x_{i+... ..._i\right) \frac{f\left(x_i\right) + f\left(x_{i+1}\right)}2$$

$$\epsffile{numinti2.eps}$$

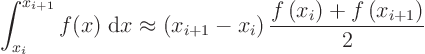
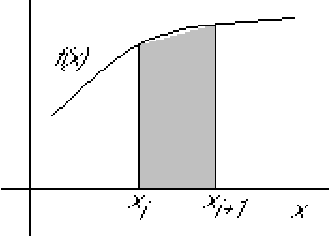
Simpson rule for an interval from $x=x_i$ to $x_{i+1}$:

$$\int_{x_i}^{x_{i+1}} f(x)\; {\rm d}x \approx \left(x_{i+... ...ght) + 4 f\big(x_{i+\frac12}\big) + f\left(x_{i+1}\right)}6$$

$$\epsffile{numinti3.eps}$$

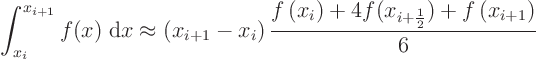
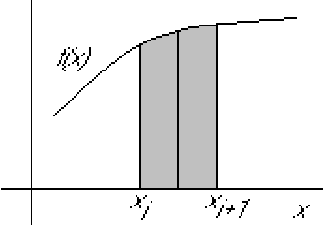
These rules are accurate if the interval from $x_i$ to $x_{i+1}$ is sufficiently small. To integrate over an interval that is not small, divide it into small ones, then integrate over each small interval and add the results.