9.2 Example

From [1, p. 205, 44], modified.

Asked:

$\begin{displaymath} \int_1^2 x \sqrt[3]{x^5 + 2x^2-1} \; {\rm d}x \end{displaymath}$

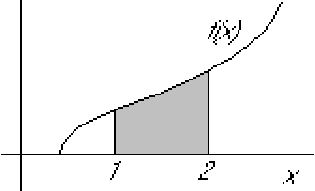
$\begin{displaymath} \epsffile{numint1.eps} \end{displaymath}$

Divide into n=2 intervals and use the trapezium rule:

$\begin{displaymath} \epsffile{numint2.eps} \end{displaymath}$

$\begin{displaymath} f(x) = x \sqrt[3]{x^5 + 2x^2-1} \end{displaymath}$

then the trapezium rule gives

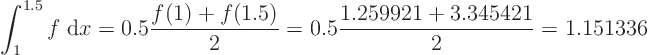
$\begin{displaymath} \int_1^{1.5} f\;{\rm d}x = 0.5 \frac{f(1)+f(1.5)}2 = 0.5 \frac{1.259921+3.345421}2 = 1.151336 \end{displaymath}$

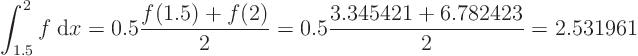
$\begin{displaymath} \int_{1.5}^2 f\;{\rm d}x = 0.5 \frac{f(1.5)+f(2)}2 = 0.5 \frac{3.345421+6.782423}2 = 2.531961 \end{displaymath}$

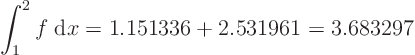
$\begin{displaymath} \int_1^{2} f\;{\rm d}x = 1.151336 + 2.531961 = 3.683297 \end{displaymath}$

Exact is 3.571639.

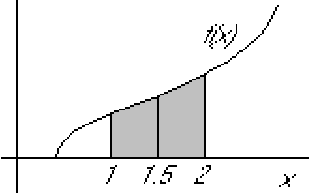
Now divide into n=2 half intervals and use the Simpson rule:

$\begin{displaymath} \epsffile{numint2.eps} \end{displaymath}$

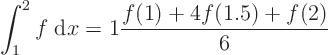
$\begin{displaymath} \int_1^{2} f\;{\rm d}x = 1 \frac{f(1)+4f(1.5) + f(2)}6 \end{displaymath}$

$\begin{displaymath} = 1 \frac{1.259921+4 * 3.345421 + 6.782423}6 = 3.570671 \end{displaymath}$

Closer to the exact value 3.571639.