17.3 More details on the extension

If your advisor actually asks you to do the above thing, your problem might of course be more complicated than my one.

One problem would be if the boundary conditions on $y$ are not homogenous. For example, if the top wall of the duct in the previous section moved horizontally with a given speed $U(t)$, you would have the boundary conditions

$$\mbox{$y=0$:}\quad u(t;0) = 0 \qquad \mbox{$y=\ell$:}\quad u(t;\ell) = U(t)$$

and the second one is not homogenous. The trick then is to write $u$ as something (anything) that satisfies the boundary conditions, and a remainder $\widetilde u$. In this case, a good choice would be

$$u = U \frac{y}{\ell} + \widetilde u$$

If you replace $u$ everywhere in the PDE and its initial and boundary conditions by the expression above, you get a problem for $\widetilde u$. That problem will have homogeneous boundary conditions, so you are back in business, now for solving for $\widetilde u$.

The next thing is finding those eigenfunctions. If $L$ is a constant times the second derivative, the eigenfunctions are sines and cosines. Then you look at the boundary conditions to figure out just which ones. But suppose you have something like

$$L \equiv a \frac{\partial^2}{\partial y^2} + b \frac{\partial}{\partial y} + c$$

What then? (Note that the coefficients $a$, $b$ and $c$ cannot depend on $t$; otherwise the usual method of separation of variables does not work. But they could and often do, depend on $y$)

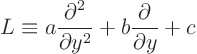
In the simplest case that $b$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 and $a$ and $c$ are constants, the eigenfunctions are still sines and cosines. The constant $c$ will just change the eigenvalues. So that is relatively trivial.

In any other case, you will need to solve the basic eigenvalue problem $LY$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\lambda Y$, an ordinary differential equation, symbolically. But if $a$, $b$ and/or $c$ depend on $y$, I never taught you how to do that! Then you will need to search through mathematical handbooks. Look under Bessel functions, Gamma function, error function, orthogonal polynomials such as those of Legendre and Hermite, etcetera. Note that you often need to play around a bit with your equation to get it in a form that you can find in the tables. Or look a bit deeper; common conversions are often mentioned somewhere.

There is now also another problem. The orthogonality property no longer applies in the form used in the previous section. There is a theorem, called the Sturm-Liouville theorem, that says that you have to find a positive solution $r$ to the differential equation

$$\frac{{\rm d}a r}{{\rm d}y} = br$$

Then you have to push this $r$, a function of $y$, inside each of the orthogonality integrals in the previous section as an additional factor:

$$f_i = \frac{\int_{y=0}^\ell Y_i(y) f(t;y) r(y) { \rm d}y}... ...r(y) { \rm d}y} {\int_{y=0}^\ell Y_i^2(y) r(y) { \rm d}y}$$

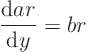
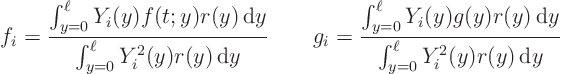
If you are in two spatial dimensions and time, you will have separate $L_y$ and $L_z$ operators. Taking $L_y$ as the simpler operator, after you switch to the basis of eigenfunctions of $L_y$, the equations for the $u_i$ will still contain both $t$ and $z$. You will now need to find the eigenfunctions of the $L_z$ operator. Note that you may be forced to include the $L_y$ eigenvalue $\lambda_i$ inside the definition of the $L_z$ operator. For example, that happens in polar coordinates, (flow in a pipe), where $y$ is the angular coordinate and $z$ the radial one. The net description of $u$ then involves terms of the form $u_{ij}(t)Y_i(y)Z_{ij}(z)$ that must be summed over both $i$ and $j$. And the orthogonality integrals become double integrals over both $y$ and $z$. All a whole lot of work, but not fundamentally different from what I told you.

As far as I can think of right now, the above covers all there is to say about the method of separation of variables. Not extremely difficult, but it sure requires a graduate student with a lot of time to carefully get all the details right.

Let me finally warn you about some common mistakes. One mistake that I see a lot is where the student leaves out an eigenfunction with eigenvalue 0. You need all the eigenfunctions. Remember that say an eigenfunction 1 is indeed a function: it is the function that is 1 at every position $y$. Another mistake that I see a lot is that a student tries to treat $f$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 or $g$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 as a number. It is a function, and you still need to write it as $f_1Y_1+f_2Y_2+\ldots$ or $g_1Y_1+g_2Y_2+\ldots$. And do the integrals. Then there are the boundary conditions. If the original problem has a boundary condition at some $y$-boundary that $Au+B\partial u/\partial y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $C$, then you should subtract a function that satisfies that boundary condition as described above. And then you should discover that the remainder $\widetilde u$ satisfies the boundary condition $A\widetilde u+B\partial\widetilde u/\partial y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0. Your eigenfunctions better satisfies that homogeneous boundary condition too, or forget it. Don't try to define an eigenfunction expansion for a time-like variable that has initial conditions. If you are tempted to do that, instead try a Laplace transform in time. That is another way to solve a lot of simple partial differential equations. For separation of variables as explained here, you really want boundary conditions for the eigenfunctions.