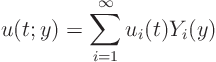|
|
|
|
|
Next: 17.3 More details on the extension |
|
Consider unsteady viscous laminar flow of, say, water, in a long and
thin horizontal two-dimensional duct. The velocity ![]() depends on the
time and the vertical position
depends on the
time and the vertical position ![]() , so
, so ![]()
![]()
![]() . However, for a
very long duct, it does not depend on the streamwise coordinate
. However, for a
very long duct, it does not depend on the streamwise coordinate ![]() .
.
According to fluid mechanics, the velocity develops according to the
equation
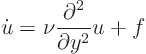
Note that so far, the above system looks almost exactly like the first
order system of ordinary differential equations in the previous
section. However, where the system of ordinary differential equations
has vectors, the scalar partial differential equation above has
functions of ![]() . The only other difference is that where the system
of ordinary differential equations had some matrix
. The only other difference is that where the system
of ordinary differential equations had some matrix ![]() , the partial
differential equation above has an
, the partial
differential equation above has an operator
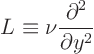
There is however one thing really different for the partial
differential equation; it has boundary conditions in ![]() . The
fluid must be at rest at the walls of the duct. With the walls at
. The
fluid must be at rest at the walls of the duct. With the walls at ![]()
![]() 0 and
0 and ![]()
![]()
![]() , (with
, (with ![]() the height of the duct),
that means
the height of the duct),
that means
Still, you can solve the partial differential equation much like the system of ordinary differential equations in the previous section. I will now show you how.
First, we need the eigenfunctions of the operator ![]() . Now a simple
second-order derivative operator has eigenfunctions that are sines and
cosines. So here the eigenfunctions could be sines or cosines of
. Now a simple
second-order derivative operator has eigenfunctions that are sines and
cosines. So here the eigenfunctions could be sines or cosines of ![]() .
But the eigenfunctions must satisfy the above boundary conditions for
.
But the eigenfunctions must satisfy the above boundary conditions for
![]() too. And these boundary conditions better be homogenous! (I will
tell you in the next section what to do if the boundary conditions for
too. And these boundary conditions better be homogenous! (I will
tell you in the next section what to do if the boundary conditions for
![]() at
at ![]()
![]() 0 and
0 and ![]()
![]()
![]() are not homogeneous.)
Fortunately, the ones above are homogeneous; there are no terms
independent of
are not homogeneous.)
Fortunately, the ones above are homogeneous; there are no terms
independent of ![]() . So we can proceed. The cosines of
. So we can proceed. The cosines of ![]() are out:
cosines are 1 at
are out:
cosines are 1 at ![]()
![]() 0, not 0. The sines are always 0 at zero,
so that is OK. But they must also be 0 at
0, not 0. The sines are always 0 at zero,
so that is OK. But they must also be 0 at ![]()
![]()
![]() , and that
only happens for
, and that
only happens for
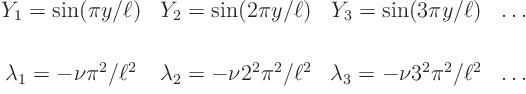
(Note that ![]()
![]()
![]() , so that is not an
additional independent eigenfunction. That is just like
, so that is not an
additional independent eigenfunction. That is just like ![]() would not be an additional eigenvector in the previous section.)
would not be an additional eigenvector in the previous section.)
Next you write everything in terms of these eigenfunctions:
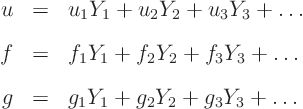
separation of variables(the one for a partial differential equation, not for an ordinary one.) Each term is separated in a function of
Once again, you have to compute these coefficients ![]() and
and ![]() . But how do you do that? You can hardly invert
an infinite
. But how do you do that? You can hardly invert
an infinite matrix
![]()
![]()
![]() of
eigenfunctions like in the previous section. Well, for an operator
like
of
eigenfunctions like in the previous section. Well, for an operator
like ![]() , just a constant multiple of the second derivative, there is
a trick: you can integrate to find them. In particular,
, just a constant multiple of the second derivative, there is
a trick: you can integrate to find them. In particular,
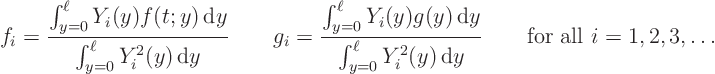
If you are astonished by that, don't be. The second derivative
operator is a real symmetric one, so in the vector case you would find
the ![]()
![]()
![]() . So you would find the
. So you would find the ![]() as the
dot product of the rows of
as the
dot product of the rows of ![]() , the eigenvectors, times the
given column vector
, the eigenvectors, times the
given column vector ![]() . In the eigenfunction case, the
dot-product summation becomes integration over
. In the eigenfunction case, the
dot-product summation becomes integration over ![]() . And the bottom
factors in the ratios above are just correction factors for the fact
that I did not normalize the eigenfunctions in any way. You can see
why the justification for the equations above is called the
orthogonality property.
. And the bottom
factors in the ratios above are just correction factors for the fact
that I did not normalize the eigenfunctions in any way. You can see
why the justification for the equations above is called the
orthogonality property.
Much like in the previous section, the basis of eigenfunctions
makes ![]() diagonal, with the eigenvalues on the main diagonal.
So the partial differential equation becomes a system of independent
equations for the coefficients of
diagonal, with the eigenvalues on the main diagonal.
So the partial differential equation becomes a system of independent
equations for the coefficients of ![]() :
:
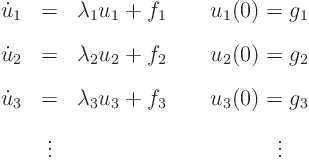
Afterwards, you can find ![]() at any time
at any time ![]() and position
and position ![]() you want
by summing:
you want
by summing: