17.1 Solution of systems using diagonalization

You should know by now how to solve a system of ordinary differential equations of the form

$$\dot{\vec u} = A \vec u + \vec f \qquad \vec u(0) = \vec g$$

where unknown vector $\vec u$ and given vector $\vec g$ depend on time, but $\vec f$ is a given constant vector and $A$ a given constant matrix. (Yes, I will use $\vec u$ instead of $\vec x$ here.) The dot of course indicates the time derivative.

However, suppose that $\dot{\vec u}$ would be replaced by the second order derivative $\ddot{\vec u}$? Like in

$$\ddot{\vec u} = A \vec u + \vec f \qquad \vec u(0) = \vec g \qquad \dot{\vec u}(0) = \vec h$$

That happens in mechanics when the forces only depend on position (no friction). Note that for this second order system we also need the initial velocities $\dot{\vec u}(0)$.

Of course, you can convert the above system to a double-size first order one. But suppose you want to keep the system size the same? Well, you can solve the system directly using the basis of eigenvectors of matrix $A$, assuming it is not defective. And the relevant matrix A is typically a real symmetric one in these applications, so never defective.

I will now show how the solution procedure works. First of course you must find the eigenvalues and eigenvectors of $A$:

$$\begin{array}{cccc} \lambda_1 & \lambda_2 & \ldots & \la... ...n \\ \vec e_1 & \vec e_2 & \ldots & \vec e_n \end{array}$$

But you always needed to do that.

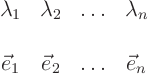
Next you write every vector in the problem in terms of the eigenvectors:

$$\begin{eqnarray*} \vec u & = & u_1' \vec e_1 + u_2' \vec e_2 + \ldots + u_n' \... ... h & = & h_1' \vec e_1 + h_2' \vec e_2 + \ldots + h_n' \vec e_n \end{eqnarray*}$$

Here the primes indicate coefficients of the vectors in the basis of eigenvectors. Note that the $u_i'$ and $f_i'$ in general depend on time but the $g_i'$ and $h_i'$ are constants, for any $i$ from 1 to $n$.

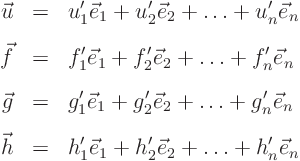
You will need to figure out what the coefficients of the given vectors $\vec f$ and $\vec g$ are now. Note that the above equations can be written in matrix form as

$$E \left(\begin{array}{c} f_1' f_2' \vdots f_n' \e... ...uad E \equiv \Big( \vec e_1, \vec e_2, \ldots \vec e_n\Big)$$

Matrix E, of course, is our transformation matrix to the basis of eigenvectors. In any case, the above equations must be solved to find the $f_i'$, $g_i'$, and $h_i'$. (In doing that, remember that for a real symmetric matrix, you take the eigenvectors orthonormal, after which the inverse matrix $E^{-1}$ is just the transpose one, $E^{\rm T}$.)

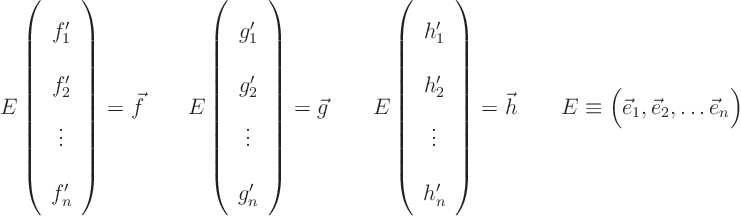
Next remember that in the basis of the eigenvectors, matrix $A$ becomes a diagonal one, with diagonal values equal to the eigenvalues. Therefore the original system of ordinary differential equations simplifies to decoupled equations:

$$\begin{eqnarray*} \ddot u_1' & = & \lambda_1 u_1' + f_1' \qquad u_1'(0) = g_... ...n u_n' + f_n' \qquad u_n'(0) = g_n' \quad \dot u_n'(0) = h_n' \end{eqnarray*}$$

You should be able to solve each of these scalar second order equations easily.

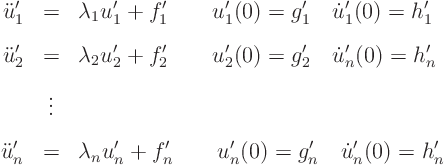
Finally you can find the solution vector $\vec u$ at any desired time by summing:

$$\vec u = u_1' \vec e_1 + u_2' \vec e_2 + \ldots + u_n' \vec e_n \equiv \sum_{i=1}^n u_i' \vec e_i$$

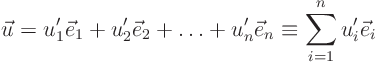
Of course, you could also solve the first order system that way. Compared to the class procedure, that has one big advantage. In the class procedure, we solved a system of equations for the variation of parameters, and one for the initial conditions. In the above method, the matrix of the two systems of equations to solve is the same, $E$, so you can use a single augmented matrix with two right hand sides (being $\vec f$ and $\vec g$). (And if $A$ is symmetric. it is easier still, because you only need to multiply by $E^{\rm T}$.)