| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
22.7 Finding the Green's functions
We can, if we want, write the solution for 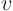 in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
The first part is due to the inhomogeneous term 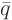 in the
partial differential equation, the second due to the initial condition
in the
partial differential equation, the second due to the initial condition
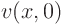

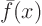
Look at the second term first, let's call it 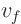 ,
,
We can substitute in the orthogonality relationship for 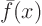 :
:
and change the order of the terms to get:
We define a shorthand symbol for the term within the square brackets:
Since this does not depend on what function 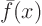 is, we can evaluate
is, we can evaluate
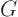 once and for all. For any
once and for all. For any 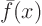 , the corresponding temperature
is then simply found by integration:
, the corresponding temperature
is then simply found by integration:
Function 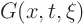 by itself is the temperature
by itself is the temperature 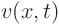 if
if 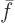 is
a single spike of heat initially located at
is
a single spike of heat initially located at 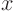

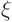 . Mathematically,
. Mathematically,
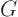 is the solution for
is the solution for 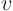 if
if 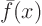 is the ``delta function''
is the ``delta function''
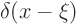 .
.
Now look at the first term in 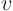 , due to
, due to 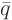 , let's call it
, let's call it 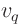 :
:
We plug in the orthogonality expression for 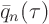 :
:
and rewrite
We see that
where the function 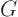 is exactly the same as it was before.
However,
is exactly the same as it was before.
However, 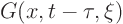 describes the temperature due to a spike
of heat added to the bar at a time
describes the temperature due to a spike
of heat added to the bar at a time 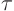 and position
and position 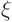 ;
it is called the Green's function.
;
it is called the Green's function.
The fact that solving the initial value problem (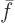 ), also
solves the inhomogeneous partial differential equation problem (
), also
solves the inhomogeneous partial differential equation problem (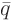 ) is known as the Duhamel principle. The idea behind this principle
is that function
) is known as the Duhamel principle. The idea behind this principle
is that function 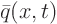 can be ``sliced up'' as a cake. The
contribution of each slice
can be ``sliced up'' as a cake. The
contribution of each slice 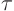
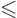
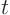
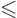
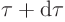 of
the cake to the solution
of
the cake to the solution 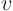 can be found as an initial value problem
with
can be found as an initial value problem
with 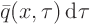 as the initial condition at time
as the initial condition at time 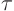 .
.
![]() in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
in other ways that may
be more efficient numerically. The solution was, rewritten more
concisely in terms of the eigenvalues and eigenfunctions:
![\begin{displaymath}
v(x,t) = \sum_n
\left[
\int_{\tau=0}^t \bar q_n(\tau)
...
...\tau
+ \bar f_n e^{-\kappa \lambda_n t}
\right]
X_n(x).
\end{displaymath}](img1701.gif)
![]() ,
,
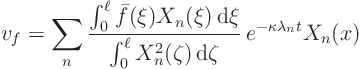
![\begin{displaymath}
v_f = \int_0^\ell
\left[
\sum_n
\frac{X_n(\xi) X_n(x...
...ta}
e^{-\kappa \lambda_n t}
\right]
\bar f(\xi) d \xi
\end{displaymath}](img1705.gif)
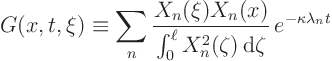
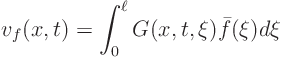
![]() , due to
, due to ![]() , let's call it
, let's call it ![]() :
:
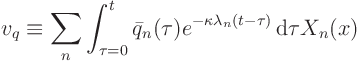
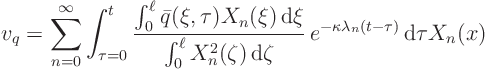
![\begin{displaymath}
v_q = \int_{\tau=0}^t \int_0^\ell
\left[
\sum_n
\fra...
...-\tau)}
\right]
\bar q(\xi,\tau) { \rm d}\xi {\rm d}\tau
\end{displaymath}](img1714.gif)
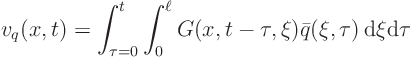
![]() ), also
solves the inhomogeneous partial differential equation problem (
), also
solves the inhomogeneous partial differential equation problem (![]() ) is known as the Duhamel principle. The idea behind this principle
is that function
) is known as the Duhamel principle. The idea behind this principle
is that function ![]() can be ``sliced up'' as a cake. The
contribution of each slice
can be ``sliced up'' as a cake. The
contribution of each slice ![]()
![]()
![]()
![]()
![]() of
the cake to the solution
of
the cake to the solution ![]() can be found as an initial value problem
with
can be found as an initial value problem
with ![]() as the initial condition at time
as the initial condition at time ![]() .
.