|
|
|
|
|
Next: 22.9 A Summary of Separation of Variables |
|
This example tries to be clever about handling inhomogeneous boundary equations for the Laplace equations. It does run into a few problems. But the students will of course explain and fix up the problem.
Find the steady temperature distribution in the square plate/cross
section below if the heat fluxes out of the sides are known.
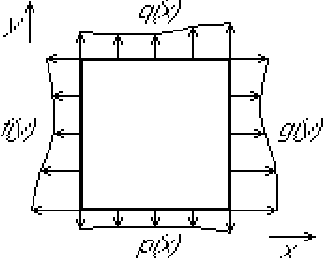
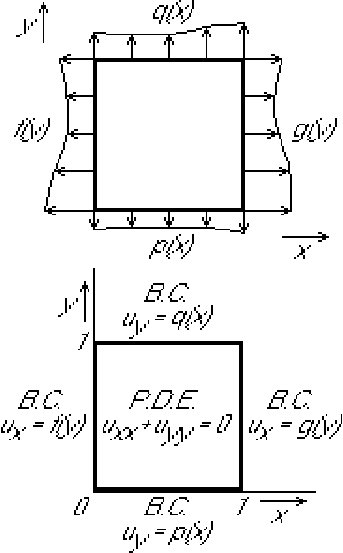
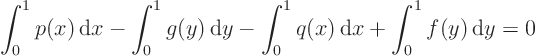
Try separation of variables:

Standard approach:
All boundary conditions are inhomogeneous. Our standard approach
would be to set ![]()
![]()
![]() where
where
This would work without any problems. A ![]() quadratic in
quadratic in ![]() would be
fine. Of course, this choice for
would be
fine. Of course, this choice for ![]() is quite arbitrary.
is quite arbitrary.
Alternative approach:
Instead, we will follow a more elegant procedure that does not
require us to arbitrarily choose a ![]() . Unfortunately, this
alternative procedure will get us into some trouble.
. Unfortunately, this
alternative procedure will get us into some trouble.
The idea is that the given problem can be seen as the sum of two problems,
each with homogeneous boundary conditions in one direction.
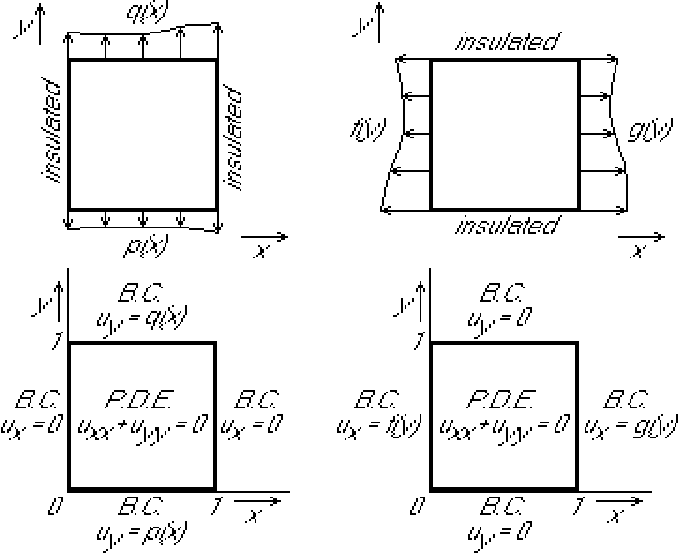
The instructor will solve the left hand problem. The students will solve the right hand problem, identify the difficulty, and fix it.
Some people split up the problem into 4, one for each side. That makes the difficulty even worse.
Substitute ![]()
![]()
![]() into the homogeneous partial
differential equation
into the homogeneous partial
differential equation ![]()
![]() 0:
0:
Since the instructor's ![]() -boundary conditions are homogeneous, he has
a Sturm-Liouville problem for
-boundary conditions are homogeneous, he has
a Sturm-Liouville problem for ![]() :
:
Expand all variables in the problem for ![]() in a Fourier series:
in a Fourier series:

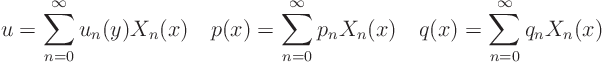
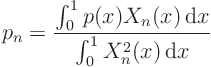
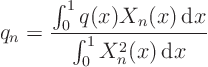
Fourier-expand the partial differential equation ![]()
![]() 0:
0:
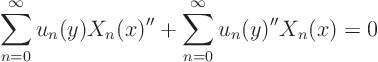
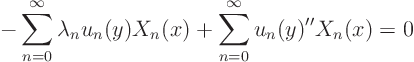
Fourier-expand the boundary condition ![]()
![]()
![]() :
:
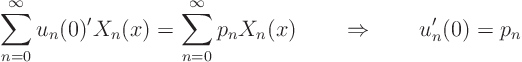
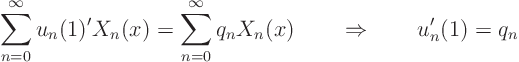
Solve the above ordinary differential equation and boundary conditions
for ![]() . It is a constant coefficient one, with a characteristic
equation
. It is a constant coefficient one, with a characteristic
equation
For ![]() the solution is
the solution is
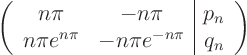
![\begin{displaymath}
u_n =
- \frac{{\rm cosh}(n\pi[y-1])}{n\pi{\rm sinh}(n\pi...
...h}(n\pi y)}{n\pi{\rm sinh}(n\pi)}q_n
\quad (n=1,2,3,\ldots)
\end{displaymath}](img1752.gif)
For ![]()
![]() 0 the solution of the ordinary differential equation is
0 the solution of the ordinary differential equation is
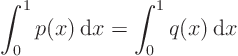
First compute the Fourier coefficients of the given boundary conditions:
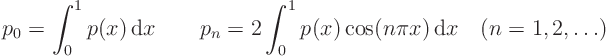
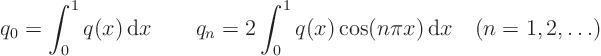
Then the solution is equal to:
![\begin{displaymath}
\begin{array}{l}
\displaystyle
u_{\strut} = A_0 + p_0 ...
...pi{\rm sinh}(n\pi)}q_n
\right]
\cos(n\pi x)
\end{array}
\end{displaymath}](img1760.gif)
But this only satisfies the boundary condition on the top of the plate if
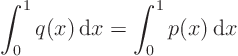
No problem! Students will explain and fix the problem.