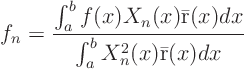| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
Subsections
22.9 A Summary of Separation of Variables
After the previous three examples, it is time to give a more
general description of the method of separation of variables.
22.9.1 The form of the solution
Before starting the process, you should have some idea of the form of
the solution you are looking for. Some experience helps here.
For example, for unsteady heat conduction in a bar of length 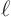 ,
with homogeneous end conditions, the temperature
,
with homogeneous end conditions, the temperature 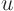 would be written
would be written
where the 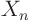 are chosen eigenfunctions and the
are chosen eigenfunctions and the 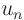 are computed
Fourier coefficients of
are computed
Fourier coefficients of 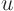 . The separation of variables
procedure allows you to choose the eigenfunctions cleverly.
. The separation of variables
procedure allows you to choose the eigenfunctions cleverly.
For a uniform bar, you will find sines and/or cosines for the functions
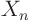 . In that case the above expansion for
. In that case the above expansion for 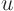 is called a Fourier
series. In general it is called a generalized Fourier series.
is called a Fourier
series. In general it is called a generalized Fourier series.
After the functions 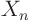 have been found, the Fourier coefficients
have been found, the Fourier coefficients
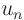 can simply be found from substituting the expression above for
can simply be found from substituting the expression above for
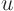 in the given partial differential equation and initial conditions.
(The boundary conditions are satisfied when you choose the
eigenfunctions
in the given partial differential equation and initial conditions.
(The boundary conditions are satisfied when you choose the
eigenfunctions 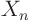 .) If there are other functions in the partial
differential equation or initial conditions, they too need to be
expanded in a Fourier series.
.) If there are other functions in the partial
differential equation or initial conditions, they too need to be
expanded in a Fourier series.
If the problem was axially symmetric heat conduction through
the wall of a pipe, the temperature would still be written
but the expansion functions 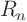 would now be found to be Bessel
functions, not sines or cosines.
would now be found to be Bessel
functions, not sines or cosines.
For heat conduction through a pipe wall without axial symmetry,
still with homogeneous boundary conditions,
the temperature would be written
where the eigenfunctions 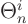 turn out to be sines and cosines
and the eigenfunctions
turn out to be sines and cosines
and the eigenfunctions 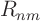 Bessel functions. Note that in the
first sum, the temperature is written as a simple Fourier series in
Bessel functions. Note that in the
first sum, the temperature is written as a simple Fourier series in
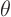 , with coefficients
, with coefficients 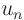 that of course depend on
that of course depend on 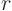 and
and
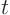 . Then in the second sum, these coefficients themselves are
written as a (generalized) Fourier series in
. Then in the second sum, these coefficients themselves are
written as a (generalized) Fourier series in 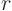 with coefficients
with coefficients
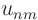 that depend on
that depend on 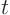 .
.
(For steady heat conduction, the coordinate ``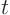 '' might actually be a
second spatial coordinate. For convenience, we will refer to
conditions at given values of
'' might actually be a
second spatial coordinate. For convenience, we will refer to
conditions at given values of 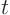 as ``initial conditions'', even
though they might physically really be boundary conditions.)
as ``initial conditions'', even
though they might physically really be boundary conditions.)
22.9.2 Limitations of the method
The problems that can be solved with separation of variables are
relatively limited.
First of all, the equation must be linear. After all, the solution is
found as an sum of simple solutions.
The partial differential equation does not necessarily have to be a
constant coefficient equation, but the coefficients cannot be too
complicated. You should be able to separate variables. A coefficient
like 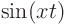 in the equation is not separable.
in the equation is not separable.
Further, the boundaries must be at constant values of the coordinates.
For example, for the heat conduction in a bar, the ends of the bar
must be at fixed locations 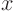
 0 and
0 and 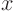

 . The bar
cannot expand, since then the end points would depend on time.
. The bar
cannot expand, since then the end points would depend on time.
You may be able to find fixes for problems such as the ones above, of
course. For example, the nonlinear Burger's equation can be converted
into the linear heat equation. The above observations apply to
straightforward application of the method.
22.9.3 The procedure
The general lines of the procedure are to choose the eigenfunctions
and then to find the (generalized) Fourier coefficients of the desired
solution 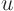 . In more detail, the steps are:
. In more detail, the steps are:
- Make the boundary conditions for the eigenfunctions
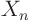 homogeneous
homogeneous
For heat conduction in a bar, this means that if nonzero end
temperatures or heat fluxes through the ends are given, you will
need to eliminate these.
Typically, you eliminate nonzero boundary conditions for the
eigenfunctions by subtracting a function 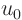 from
from 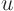 that
satisfies these boundary conditions. Since
that
satisfies these boundary conditions. Since 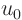 only needs to
satisfy the boundary conditions, not the partial differential
equation or the initial conditions, such a function is easy to find.
only needs to
satisfy the boundary conditions, not the partial differential
equation or the initial conditions, such a function is easy to find.
If the boundary conditions are steady, you can try subtracting the
steady solution, if it exists. More generally, a low degree
polynomial can be tried, say 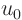

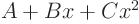 , where the
coefficients are chosen to satisfy the boundary conditions.
, where the
coefficients are chosen to satisfy the boundary conditions.
Afterwards, carefully identify the partial differential equation and
initial conditions satisfied by the new unknown 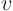

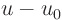 . (They are
typically different from the ones for
. (They are
typically different from the ones for 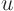 .)
.)
- Identify the eigenfunctions
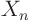
To do this substitute a single term 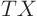 into the homogeneous
partial differential equation. Then take all terms involving
into the homogeneous
partial differential equation. Then take all terms involving 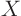 and the corresponding independent variable to one side of the
equation, and
and the corresponding independent variable to one side of the
equation, and 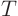 and the other independent variables to the other
side. (If that turns out to be impossible, the partial differential
equation
cannot be solved using separation of variables.)
and the other independent variables to the other
side. (If that turns out to be impossible, the partial differential
equation
cannot be solved using separation of variables.)
Now, since the two sides of the equation depends on different
coordinates, they must both be equal to some constant. The constant
is called the eigenvalue.
Setting the 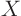 -side equal to the eigenvalue gives an ordinary
differential equation. Solve it to get the eigenfunctions
-side equal to the eigenvalue gives an ordinary
differential equation. Solve it to get the eigenfunctions 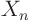 .
In particular, you get the complete set of eigenfunctions
.
In particular, you get the complete set of eigenfunctions 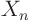 by
finding all possible solutions to this ordinary differential
equation. (If the ordinary differential equation problem for the
by
finding all possible solutions to this ordinary differential
equation. (If the ordinary differential equation problem for the
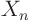 turns out to be a regular Sturm-Liouville problem of the type
described in the next section, the method is guaranteed to work.)
turns out to be a regular Sturm-Liouville problem of the type
described in the next section, the method is guaranteed to work.)
The equation for 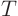 is usually safest ignored. The book tells you
to also solve for the
is usually safest ignored. The book tells you
to also solve for the 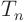 , to get the Fourier coefficients
, to get the Fourier coefficients 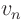 ,
but if you have an inhomogeneous partial differential equation, you
have to mess around to get it right. Also, it is confusing, since
the eigenfunctions
,
but if you have an inhomogeneous partial differential equation, you
have to mess around to get it right. Also, it is confusing, since
the eigenfunctions 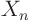 do not have undetermined constants,
but the coefficients
do not have undetermined constants,
but the coefficients 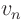 do. It are the undetermined
constants in
do. It are the undetermined
constants in 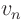 that allow you to satisfy the initial conditions.
They probably did not make this fundamental difference between the
functions
that allow you to satisfy the initial conditions.
They probably did not make this fundamental difference between the
functions 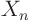 and the
coefficients
and the
coefficients 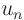 clear in your undergraduate classes.
clear in your undergraduate classes.
There is one case in which you do need to use the equation for the
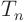 : in problems with more than two independent variables, where
you want to expand the
: in problems with more than two independent variables, where
you want to expand the 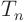 themselves in a generalized Fourier
series. That would be the case for the pipe wall without axial
symmetry. Simply repeat the above separation of variables process
for the partial differential equation satisfied by the
themselves in a generalized Fourier
series. That would be the case for the pipe wall without axial
symmetry. Simply repeat the above separation of variables process
for the partial differential equation satisfied by the 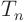 .
.
- Find the coefficients
Now find the Fourier coefficients 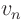 (or
(or 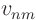 for three
independent variables) by putting the Fourier series expansion into
the partial differential equation and initial conditions.
for three
independent variables) by putting the Fourier series expansion into
the partial differential equation and initial conditions.
While doing this, you will also need to expand the inhomogeneous
terms in the partial differential equation and initial conditions
into a Fourier series of the same form. You can find the
coefficients of these Fourier series using the
orthogonality property described in the next section.
You will find that the partial differential equation produces
ordinary differential equations for the individual coefficients.
And the integration constants in solving those equations follow from
the initial
conditions.
Afterwards you can play around with the solution to get other
equivalent forms. For example, you can interchange the order of
summation and integration (which results from the orthogonality
property) to put the result in a Green's function form, etcetera.
22.9.4 More general eigenvalue problems
So far, the eigenvalue problems in the examples were of the form
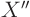

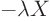 . But you might get a different problem in other
examples. Usually that produces a different orthogonality expression.
. But you might get a different problem in other
examples. Usually that produces a different orthogonality expression.
You can figure out what is the correct expression by writing your
ordinary differential equation in the standard form of a
Sturm-Liouville problem:
where 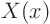 is the eigenfunction to be found and
is the eigenfunction to be found and 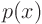
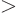 0,
0, 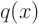 ,
and
,
and 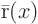
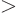 0 are given functions. The distinguishing
feature is that the coefficient of the second,
0 are given functions. The distinguishing
feature is that the coefficient of the second, 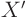 , term is the
derivative of the coefficient of the first,
, term is the
derivative of the coefficient of the first, 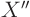 term.
term.
Starting with an arbitrary second order linear ordinary differential
equation, you can achieve such a form by multiplying the entire
ordinary differential equation with a suitable factor.
The boundary conditions may either be periodic ones,
or they can be homogeneous of the form
where 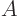 ,
, 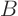 ,
, 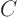 , and
, and 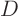 are given constants. Note the important
fact that a Sturm-Liouville problem must be completely homogeneous:
are given constants. Note the important
fact that a Sturm-Liouville problem must be completely homogeneous:
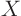
 0 must be a solution.
0 must be a solution.
If you have a Sturm-Liouville problem, simply (well, simply ...) solve
it. The solutions only exists for certain values of 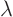 . Make
sure you find all solutions, or you are in trouble. They will
form an infinite sequence of `eigenfunctions', say
. Make
sure you find all solutions, or you are in trouble. They will
form an infinite sequence of `eigenfunctions', say 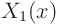 ,
, 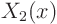 ,
,
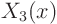 , ... with corresponding `eigenvalues'
, ... with corresponding `eigenvalues' 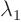 ,
, 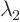 ,
,
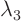 , ... that go off to positive infinity.
, ... that go off to positive infinity.
You can represent arbitrary functions, say 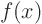 , on the
interval
, on the
interval ![$[a,b]$](img1780.gif) as a generalized Fourier series:
as a generalized Fourier series:
If you know 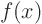 , the orthogonality relation that gives the generalized
Fourier coefficients
, the orthogonality relation that gives the generalized
Fourier coefficients 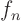 is
is
Now you know why you need to write your Sturm-Liouville problem in
standard form: it allows you to pick out the weight factor
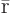 that you need to put in the orthogonality relation!
that you need to put in the orthogonality relation!
![]() ,
with homogeneous end conditions, the temperature
,
with homogeneous end conditions, the temperature ![]() would be written
would be written
![]() . In that case the above expansion for
. In that case the above expansion for ![]() is called a Fourier
series. In general it is called a generalized Fourier series.
is called a Fourier
series. In general it is called a generalized Fourier series.
![]() have been found, the Fourier coefficients
have been found, the Fourier coefficients
![]() can simply be found from substituting the expression above for
can simply be found from substituting the expression above for
![]() in the given partial differential equation and initial conditions.
(The boundary conditions are satisfied when you choose the
eigenfunctions
in the given partial differential equation and initial conditions.
(The boundary conditions are satisfied when you choose the
eigenfunctions ![]() .) If there are other functions in the partial
differential equation or initial conditions, they too need to be
expanded in a Fourier series.
.) If there are other functions in the partial
differential equation or initial conditions, they too need to be
expanded in a Fourier series.
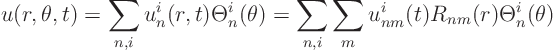
![]() '' might actually be a
second spatial coordinate. For convenience, we will refer to
conditions at given values of
'' might actually be a
second spatial coordinate. For convenience, we will refer to
conditions at given values of ![]() as ``initial conditions'', even
though they might physically really be boundary conditions.)
as ``initial conditions'', even
though they might physically really be boundary conditions.)
![]() in the equation is not separable.
in the equation is not separable.
![]()
![]() 0 and
0 and ![]()
![]()
![]() . The bar
cannot expand, since then the end points would depend on time.
. The bar
cannot expand, since then the end points would depend on time.
![]() . In more detail, the steps are:
. In more detail, the steps are:
![]()
![]()
![]() . But you might get a different problem in other
examples. Usually that produces a different orthogonality expression.
. But you might get a different problem in other
examples. Usually that produces a different orthogonality expression.
![]() . Make
sure you find all solutions, or you are in trouble. They will
form an infinite sequence of `eigenfunctions', say
. Make
sure you find all solutions, or you are in trouble. They will
form an infinite sequence of `eigenfunctions', say ![]() ,
, ![]() ,
,
![]() , ... with corresponding `eigenvalues'
, ... with corresponding `eigenvalues' ![]() ,
, ![]() ,
,
![]() , ... that go off to positive infinity.
, ... that go off to positive infinity.
![]() , on the
interval
, on the
interval ![]() as a generalized Fourier series:
as a generalized Fourier series: