|
|
|
|
|
Next: 22.11 A Problem in Three Independent Variables |
|
In the simplest problems, the eigenfunctions are sines and cosines. That includes the examples so far. But it is quite easy to get different eigenfunctions. In this example, they will turn out to be products of sines and exponentials.
Find the unsteady temperature distribution in the moving bar below for arbitrary position and time if the initial distribution at time zero and the temperatures of the ends are known.
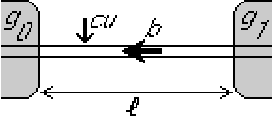
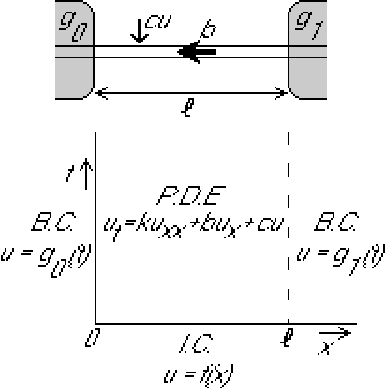
Try separation of variables:
The ![]() -boundary conditions are inhomogeneous:
-boundary conditions are inhomogeneous:
So we try finding a ![]() satisfying these boundary conditions:
satisfying these boundary conditions:
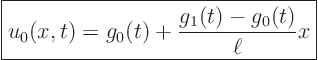
To get rid of the inhomogeneous boundary conditions, we subtract
![]() from
from ![]() . That will produce homogeneous boundary conditions for
the remainder
. That will produce homogeneous boundary conditions for
the remainder ![]()
![]()
![]() . Indeed, if you plug
. Indeed, if you plug ![]()
![]()
![]() into the boundary conditions, you get
into the boundary conditions, you get
Substitute ![]()
![]()
![]() into the partial differential equation
into the partial differential equation
![]()
![]()
![]() to get
to get
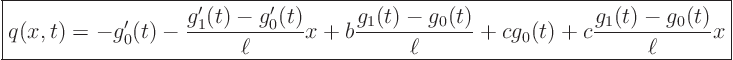
Substitute ![]()
![]()
![]() into the initial condition
into the initial condition ![]()
![]()
![]() :
:
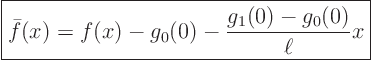
The problem for ![]() is therefor:
is therefor:
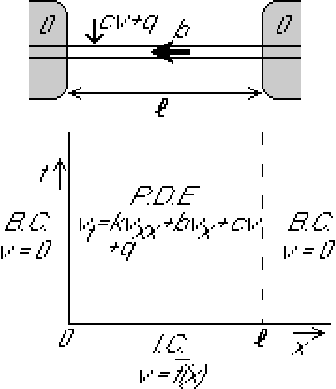
Substitute ![]()
![]()
![]() into the homogeneous partial
differential equation
into the homogeneous partial
differential equation ![]()
![]()
![]() :
:
The Sturm-Liouville problem for ![]() is now:
is now:
This is a constant coefficient ordinary differential equation, with a
characteristic polynomial:
Roots ![]() and
and ![]() real and distinct:
real and distinct:
Boundary conditions:
Since ![]()
![]()
![]()
![]()
![]() :
:
Boundary conditions:
For convenience, we will write the roots of the characteristic
polynomial more concisely as:
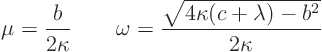
Boundary conditions:
Nontrivial solutions ![]() can only occur if
can only occur if
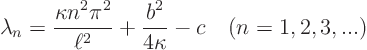
Also, choosing each ![]()
![]() 1:
1:
Expand all variables in the problem for ![]() in a Fourier series:
in a Fourier series:

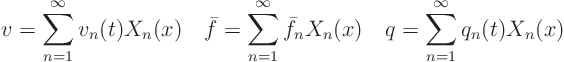
We want to first find the Fourier coefficients of the known functions
![]() and
and ![]() . Unfortunately, the ordinary differential equation
found in the previous section,
. Unfortunately, the ordinary differential equation
found in the previous section,
Having found ![]() , we can write the orthogonality
relationships for the generalized Fourier coefficients of
, we can write the orthogonality
relationships for the generalized Fourier coefficients of ![]() and
and
![]() (remember that
(remember that ![]()
![]()
![]() ):
):
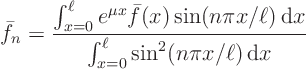
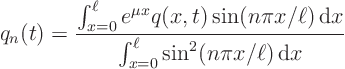
Expand the partial differential equation ![]()
![]()
![]() in a generalized Fourier series:
in a generalized Fourier series:
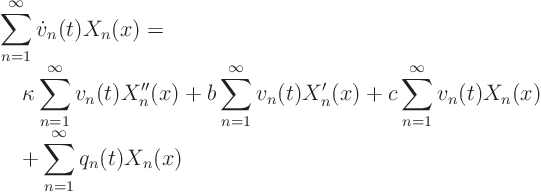
Because of the choice of the ![]() ,
, ![]()
![]()
![]() :
:
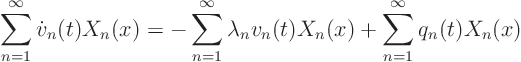
Expand the initial condition ![]()
![]()
![]() in a
generalized Fourier series:
in a
generalized Fourier series:
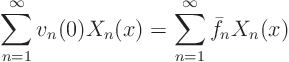
Solve this ordinary differential equation and initial condition for ![]() :
:
Homogeneous equation:
Inhomogeneous equation:
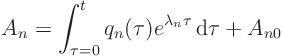
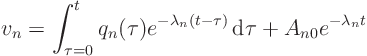
Initial condition: ![]()
![]()
![]() .
.
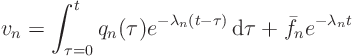
Total solution:
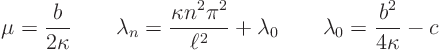
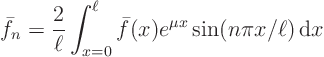
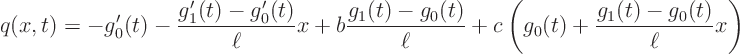
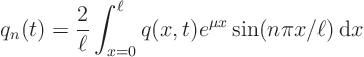
![\begin{displaymath}
\begin{array}{l}
\displaystyle
u_{\strut} = g_0(t) + \...
..._n t}
\right]
e^{- \mu x} \sin(n\pi x/\ell)
\end{array}
\end{displaymath}](img1850.gif)
Define a new unknown ![]() by
by ![]()
![]()
![]() .
Put this in the partial differential equation for
.
Put this in the partial differential equation for ![]() and choose
and choose
![]() and
and ![]() so that the
so that the ![]() and
and ![]() terms drop out. This
requires:
terms drop out. This
requires:
Then:
No fun! Note that the generalized Fourier series coefficients for ![]() become normal Fourier coefficients for
become normal Fourier coefficients for ![]() .
.