5.1 Introduction

Combined changes in variables are common. For example:

• Error estimates.
• Changes for a moving particle in a field.
• Changes in scalar quantities depending on several variables,
• ...

The key concept is the total differential. For any function $f$ $\vphantom0\raisebox{1.5pt}{$=$}$ $f(x,y,z)$,

$${\rm d}f = \frac{\partial f}{\partial x} {\rm d}x + \f... ...artial y} {\rm d}y + \frac{\partial f}{\partial z} {\rm d}z$$

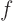
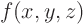Of course, 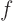$f$ could be a vector.