|
|
|
|
|
Next: 5.3 Example |
|
From [1, p. 422, 27a]
Given:
![\begin{displaymath}
\omega = \sqrt[3]{\frac gb}
\end{displaymath}](img156.gif)
Asked:
The maximum percentage error in ![]() .
.
Given is that the maximum error in ![]() is
is ![]() and the maximum error
in
and the maximum error
in ![]() is
is ![]() . That means that the relative errors
are:
. That means that the relative errors
are:
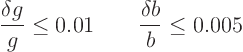
Error manipulation rules:
Consider first the relative change in ![]() due to changes
due to changes
![]() in
in ![]() and
and ![]() in
in ![]() . The rule for differentiating
a ratio implies:
. The rule for differentiating
a ratio implies:
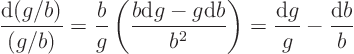
Note that if you do not know the sign of the errors, you can only
say that the final result is no bigger than
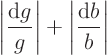
Hence the greatest possible relative error in ![]() is:
is:
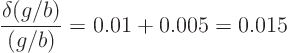
But we need the relative error in ![]() instead of in
instead of in ![]() .
Denoting
.
Denoting ![]() by
by ![]() for now, the rule for differentiating a
power gives
for now, the rule for differentiating a
power gives
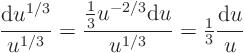
Hence