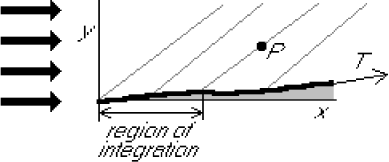
| Supersonic flow over a membrane. |
|
|
|
We need to find the original to
Looking in the tables:
The other factor is a shifted function 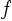 , restricted to the interval
that its argument is positive:
, restricted to the interval
that its argument is positive:
With the bar, I indicate that I only want the part of the function for
which the argument is positive. This could be written instead as
where the Heaviside step function 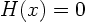 if
if 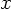 is negative and 1 if
it is positive.
is negative and 1 if
it is positive.
Figure 34:
Function 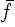 .
.
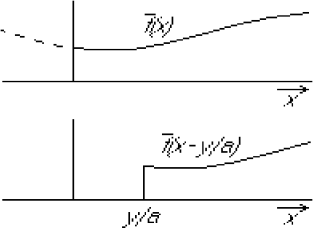 |
Use convolution, Table 6.3, # 7. again to get the product.
This must be cleaned up. I do not want bars or step functions
in my answer.
I can do that by restricting the range of integration to only those
values for which  is nonzero. (Or
is nonzero. (Or  is nonzero, if you
prefer)
is nonzero, if you
prefer)
Figure 35:
Function 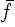 .
.
 |
Two cases now exist:
It is neater if the integration variable is the argument of 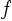 . So,
define
. So,
define
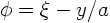 and convert:
and convert:
This allows me to see which physical 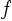 values I actually integrate
over when finding the flow at an arbitrary point:
values I actually integrate
over when finding the flow at an arbitrary point:
Figure 5:
Supersonic flow over a membrane.
 |
![]() , restricted to the interval
that its argument is positive:
, restricted to the interval
that its argument is positive:
![]() is nonzero. (Or
is nonzero. (Or ![]() is nonzero, if you
prefer)
is nonzero, if you
prefer)
![]() . So,
define
. So,
define
![]() and convert:
and convert: