4 Formulae for substances

How you treat a substance depends on the type of substance.

4.1 Substances with B-tables

Tables of specific properties such as tables B.1.1-B.1.4 for water are available. Use requires normally drawing $pv$- and $Tv$- or $Ts$-diagrams, which students must master, and which is covered elsewhere.

In the two phase region:

$$v=v_f + x \left(v_g -v_f\right) \quad u=u_f + x \left(u_... ...\left(h_g -h_f\right) \quad s=s_f + x \left(s_g -s_f\right)$$

where $f$ stands for the saturated liquid ($x=0$) value at the same pressure and same temperature, and $g$ for the saturated vapor ($x=1$) value. These can be found in the Appendix B tables. The quality $x$ is the ratio of the vapor mass to the total mass of vapor and liquid. The quality $x$ is undefined if the substance is not two-phase or saturated.

For compressed liquids, often there are no suitable tables available. Fortunately, good approximate values for $v$, $u$, $s$, and $h$ can usually be taken from the saturated tables at the correct given temperature. The fact that the given pressure is not the same as the saturated pressure must then be ignored. (For $h$, it is more accurate to write $h=u+pv$ and then take $u$ and $v$ from the saturated tables, instead of $h$ itself.)

4.2 Ideal Gases

Specific gas constant $R$ in terms of the universal gas constant $\bar R$ (table A.1):

$$R = \frac {\bar R}{M}$$

where $M$ is the molecular mass (table A.5, but this table already includes $R$).

Forms of the ideal gas law:

$$\begin{array}{cc} pv = RT \quad & \quad p\bar v = \bar R... ... pV = m R T \quad & \quad p V = \bar n \bar R T \end{array}$$

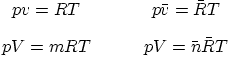
To correct for real gas effects, replace $R$ (or $\bar R$) by $Z R$ ($Z\bar R$), where $Z$ is the compressibility factor (figure D1, with $P_r=p/p_c$, $T_r=T/T_c$.)

For an ideal gas, $u$, $h$, $C_p$, $C_v$, and $k$ only depend on temperature. Also,

$$u_2 - u_1 = \int_1^2 C_v \;{\rm d}T \qquad h_2 - h_1 = \int_1^2 C_p \;{\rm d}T \qquad$$

(Using table A.6, these can actually be integrated.) Note that for ideal gasses we often do not have $u$, $h$, or $s$ themselves, and we have to make do with differences. (For a mixing chamber you will need to replace $\dot m_3$ with $\dot m_1 + \dot m_2$ before you can use differences.)

Specific heat relation:

$$C_p - C_v = R$$

Hence if we know $C_p$ (tables A.5 or A.6) we can compute $C_v$ and vice-versa. Also, if $C_p$ is constant, then so is $C_v$ and vice-versa,

Definition of specific heat ratio:

$$k = \frac{C_p}{C_v}$$

If $k$ is constant, then so are $C_p$ and $C_v$, and vice-versa.

Note that isothermal ideal gasses are also polytropic with $n=1$.

4.2.1 Ideal gasses in A.7.1 or A8

The internal energy $u$ and enthalpy $h$ can be read off in the table as a function of temperature. Or vice-versa, for that matter.

The formula that gives you the entropy $s$ is, (in terms of differences),

$$s_2 - s_1 = s_{T2}^0-s_{T1}^0 - R \ln\left(\frac{p_2}{p_1}\right)$$

where $s_{T1}^0$, also written as $s_T^0(T_1)$, is whatever you find in the table's $s_T^0$ column at the temperature $T_1$. (It is what the entropy would be if the pressure would have been one atmosphere.)

4.2.2 Ideal gasses with constant specific heats

If no A.7.1/A.8 table is available, you will have to assume that the specific heats $C_p$ and $C_v$, as well as their ration $k$ are constant. Specific heats that can be assumed to be approximately constant can be computed from the average process temperature using table A.6. Less accurately, near room temperature they can be taken from A.5. Use A.6 wherever possible unless you are very close to room temperature.

Internal energy:

$$u_2 - u_1 \approx {C_v}\strut_{\mbox{\scriptsize ave}} \left(T_2 - T_1\right)$$

Enthalpy:

$$h_2 - h_1 \approx {C_p}\strut_{\mbox{\scriptsize ave}} \left(T_2 - T_1\right)$$

Entropy:

$$\begin{array}{rcl} s_2 - s_1 & = & \displaystyle C_p\s... ...criptsize ave}} \ln\left(\frac{v_2}{v_1}\right) \end{array}$$

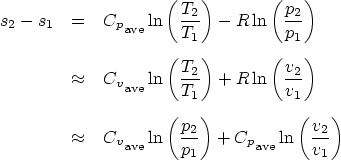
If the process is isothermal or reversible adiabatic (isentropic), the following “polytropic” relations also apply (they are equivalent to the equations above, but often much more convenient):

$$\begin{array} {l@{\hspace{6pt}}c@{\hspace{6pt}}c@{\hspac... ...frac{T_1}{T_2}\right)^{\textstyle\frac{1}{n-1}} \end{array}$$

4.3 Solids and Liquids without B-tables

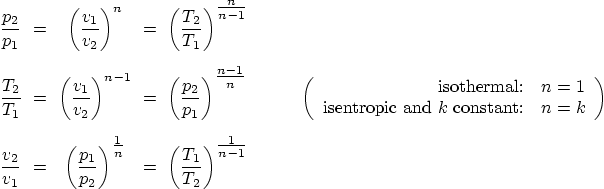
Approximate formulae if no better tabulated values are available, or to simplify things.

Heat added:

$$\vphantom{Q}_1Q_2 = m \int_1^2 C_{(p)} \;{\rm d}T \approx ... ..._{(p)}}\strut_{\mbox{\scriptsize ave}} \left(T_2 - T_1\right)$$

Enthalpy:

$$h_2-h_1 \approx {C_{(p)}}\strut_{\mbox{\scriptsize ave}} ... ...(T_2 - T_1\right)\quad \left[ + v\left(p_2-p_1\right) \right]$$

The term in the square brackets can often be neglected.

Entropy:

$$s_2 - s_1 \approx {C_{(p)}}\strut_{\mbox{\scriptsize ave}} \ln\left(\frac{T_2}{T_1}\right)$$