Developed

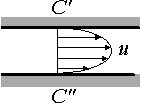
$\begin{displaymath} \hbox{\epsffile{figures/develop.ps}} \end{displaymath}$

At and beyond station C the flow is called developed. We will assume that the flow is nonturbulent and that the streamlines have become parallel. These assumptions allow us to solve the incompressible Navier-Stokes equations exactly!

Note that for parallel streamlines, (unidirectional flow), .

Continuity:

$\begin{displaymath} \mbox{div}\left(\vec v\right) = 0 = \frac{\partial u}{\par... ...frac{\partial v}{\partial y} \quad\Longrightarrow\quad u=u(y) \end{displaymath}$

-momentum:

$\begin{displaymath} \rho \rlap{\kern 3pt\smash{\Bigg/}}\frac{Dv}{Dt} = - \rho g... ...ash{\bigg/}} v \quad\Longrightarrow\quad p = -\rho g y + P(x) \end{displaymath}$

-momentum:

$\begin{displaymath} \rho \rlap{\kern 3pt\smash{\Bigg/}}\frac{\partial u}{\parti... ...u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) \end{displaymath}$

hence:

$\begin{displaymath} \frac{\mbox{d}^2 u}{\mbox{d}y^2} = \frac{1}{\mu} \frac{\mbox{d}P}{\mbox{d}x} = \mbox{ constant } \end{displaymath}$

Exercise:

Why is it constant? If the duct is long, how can you approximate the constant? What is the sign of $\mbox{d}P/\mbox{d}x$ ?

$\bullet$

$\begin{displaymath} \frac{\mbox{d}u}{\mbox{d}y} = \frac{1}{\mu} \frac{\mbox{d}P}{\mbox{d}x} y + A \end{displaymath}$

$\begin{displaymath} u = \frac{1}{2\mu} \frac{\mbox{d}P}{\mbox{d}x} y^2 + A y + B \end{displaymath}$

$\begin{displaymath} \hbox{\epsffile{figures/develop.ps}} \end{displaymath}$

The boundary conditions give the constants:

$\begin{displaymath} \fbox{$\displaystyle \frac{\mbox{d}P}{\mbox{d}x} = \mbox{c... ...\rho g y + \frac{\mbox{d}P}{\mbox{d}x} x + \mbox{constant} $} \end{displaymath}$

Maximum velocity:

$\begin{displaymath} v_{\mbox{max}} = - \frac{h^2}{8\mu} \frac{\mbox{d}P}{\mbox{d}x} \qquad u = \frac{4(h-y) y}{h^2} v_{\mbox{max}} \end{displaymath}$

Mass flux (per unit span):

$\begin{displaymath} \dot m = \int \rho \vec v \cdot \vec n \d S = \int_0^h \rho u \d y = {\textstyle\frac{2}{3}} \rho v_{\mbox{max}} h \end{displaymath}$

The volumetric flow rate $Q = \dot m/\rho$

Average velocity:

$\begin{displaymath} \fbox{$\displaystyle \dot m \equiv \rho Q \equiv \rho v_{\... ...ad v_{\mbox{ave}} = {\textstyle\frac{2}{3}} v_{\mbox{max}} $} \end{displaymath}$

Note that $Q=v_{\mbox{ave}} h$ and $\dot m=\rho v_{\mbox{ave}} h$ .

$\begin{displaymath} \fbox{$\displaystyle \frac{\mbox{d}P}{\mbox{d}x} = - \frac{12\mu}{h^2} v_{\mbox{ave}} $} \end{displaymath}$

Vorticity:

$\begin{displaymath} \vec\omega = \hat k \left( \rlap{\kern 3pt\smash{\Bigg/}}... ...ht) = \hat k\frac{1}{2\mu} \frac{\mbox{d}P}{\mbox{d}x} (h-2y) \end{displaymath}$

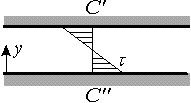
Shear:

$\begin{displaymath} \tau \equiv \tau_{xy} = \mu \left( \rlap{\kern 3pt\smash{... ...} \right) = - \frac{1}{2} \frac{\mbox{d}P}{\mbox{d}x} (h-2y) \end{displaymath}$

$\begin{displaymath} \hbox{\epsffile{figures/shear.ps}} \end{displaymath}$

Exercise:

Verify the integral momentum equation for any duct length .

What is the rate of change of linear momentum inside?
What is the net outflow of momentum through the boundary?
What are the forces on the control volume?

$\bullet$

Note that this flow becomes turbulent at a Reynolds number of say 1,500 (in the range from 1,000 to 8,000). The above expressions do not apply to turbulent flow.