Head Loss

Steady incompressible flows through pipes are very important for many applications. In the simplest case we will have a single duct with a mass flux $\dot m=\rho Q = \rho v S$ through it:

$$\hbox{\epsffile{figures/massflux.ps}}$$

Note that according to continuity, $\dot m$ is constant, so that the average velocity $v$ increases when $S$ becomes smaller.

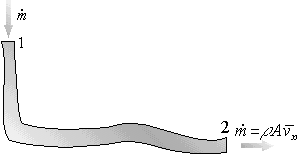
Ideally, the flow would be inviscid (no dissipation) and in each cross section the velocity, pressure and the height would be constant. In that case the Bernoulli law applies as:

$$\frac{p_2}{\rho} + {\textstyle\frac{1}{2}} v_2^2 + g h_2 = ... ...rho} + {\textstyle\frac{1}{2}} v_1^2 + g h_1 = \mbox{constant}$$

In real flows with dissipation and nonuniform velocity in the cross sections, we can write

$$\frac{p_2}{\rho} + {\textstyle\frac{1}{2}} \alpha_2 v_2^2 +... ...}{\rho} + {\textstyle\frac{1}{2}} \alpha_1 v_1^2 + g h_1 - h_l$$

where $h_l$ is the head loss, the effect of irreversible dissipation of energy. Also, ${\textstyle\frac{1}{2}} \alpha v^2$ is the average kinetic energy per unit mass of the fluid at the cross section; $\alpha = 1$ as long as the flow is uniform at the cross section. For the developed duct with the parabolic profile, $\alpha = 54/35 \approx 1.5$. For laminar pipe flow, $\alpha = 2$. For turbulent flows, $\alpha$ is usually not very far from 1. Finally, $p$ and $h$ are the average pressure and height of the cross section.

Note: The above equation can be derived by integrating the mechanical energy equation over the duct. It may then be verified that all averages are weighted over the mass flux. The exception is $v$, which is still the plain average velocity.

Note: When treating air at low velocities as incompressible, use a single density: do not use $p_1/\rho_1$ and $p_2/\rho_2$, even if both densities are known precisely.

Note: Conventionally head loss is expressed in units of height, by dividing the head loss above by $g$. (In particular, $gh$ becomes $h$.) That makes the head loss equal to the height loss of a manometer measuring the head loss, assuming the manometer is filled with the same fluid.