Values

Typical head loss values for important situations may be found in tables. For bends and area changes, they can be expressed as a head loss coefficient: $h_l = K {\textstyle\frac{1}{2}} v_{\mbox{ref}}^2$.

$$\hbox{\epsffile{figures/constric.ps}} \qquad \hbox{\epsffile{figures/constri2.ps}}$$

Exercise:

Why express the headloss in terms of ${\textstyle\frac{1}{2}} v_{\mbox{ref}}^2$? Why not, say, $p_{\mbox{ref}}/\rho$?

$\bullet$

For the developed two-dimensional duct flow in the previous subsection, the head loss over a distance $L$ of the duct is:

$$\frac{p_2}{\rho} + {\textstyle\frac{1}{2}} \rlap{\kern 0pt\... .../}}\alpha_1 v_1^2 + g \rlap{\kern -1pt\smash{\bigg/}}h_1 - h_l$$

$$\hbox{\epsffile{figures/conarea.ps}}$$

$$h_l = \frac{p_1-p_2}{\rho} = -\frac{1}{\rho} \frac{\mbox{d}... ...{ave}} h} {\textstyle\frac{1}{2}} v_{\mbox{ave}}^2 \frac{L}{h}$$

This head loss (called major head loss) can be given in terms of a friction factor:

$$\fbox{$\displaystyle f_{\mbox{laminar duct}} = \frac{24\m... ..._{\mbox{ave}} h} = \frac{24}{Re_h} \qquad K = f \frac{L}{h}$}$$

For laminar flow in a circular pipe,

$$\fbox{$\displaystyle f_{\mbox{laminar pipe}} = \frac{64}{Re_D}$}$$

There will be an additional head loss for the entrance effects (called minor head loss):

$$\hbox{\epsffile{figures/inlet.ps}}$$

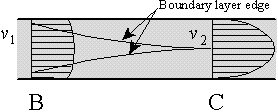
For the duct exit, the kinetic energy will probably be mostly lost:

$$\hbox{\epsffile{figures/separate.ps}}$$