| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.2 Some Green’s functions
D.2.1 The Poisson equation
The so-called Poisson equation
is
Here  is supposed to be a given function and
is supposed to be a given function and 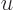 an unknown function
that is to be found.
an unknown function
that is to be found.
The solution 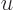 to the Poisson equation in infinite space may be
found in terms of its so-called
to the Poisson equation in infinite space may be
found in terms of its so-called Green’s function
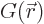 . In particular:
. In particular:
Loosely speaking, the above integral solution chops function  up
into spikes
up
into spikes 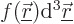 . A spike at a position
. A spike at a position 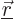 then makes a contribution
then makes a contribution 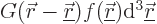 to
to 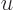 at
at
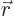 . Integration over all such spikes gives the complete
. Integration over all such spikes gives the complete
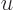 .
.
Note that often, the Poisson equation is written without a minus sign.
Then there will be a minus sign in 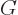 .
.
The objective is now to derive the above Green’s function. To do
so, first an intuitive derivation will be given and then a more
rigorous one. (See also chapter 13.3.4 for a more physical
derivation in terms of electrostatics.)
The intuitive derivation defines 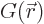 as the solution due to a
unit spike, i.e. a
as the solution due to a
unit spike, i.e. a delta function,
located at the
origin. That means that 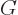

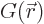 is the solution to
is the solution to
Here 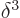

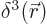 is the three-dimensional delta function,
defined as an infinite spike at the origin that integrates to 1.
is the three-dimensional delta function,
defined as an infinite spike at the origin that integrates to 1.
By itself the above definition is of course meaningless: infinity is
not a valid number. To give it meaning, it is necessary to define an
approximate delta function, one that is merely a large spike rather
than an infinite one. This approximate delta function
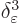

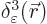 must still integrate
to 1 and will be required to be zero beyond some small distance
must still integrate
to 1 and will be required to be zero beyond some small distance
 from the origin:
from the origin:
In the above integral the region of integration should at least
include the small region of radius  around the origin.
The approximate delta function will further be assumed to be
nonnegative. It must have large values in the small vicinity around
the origin where it is nonzero; otherwise the integral over the small
vicinity would be small instead of 1. But the key is that the values
are not infinite, just large. So normal mathematics can be used.
around the origin.
The approximate delta function will further be assumed to be
nonnegative. It must have large values in the small vicinity around
the origin where it is nonzero; otherwise the integral over the small
vicinity would be small instead of 1. But the key is that the values
are not infinite, just large. So normal mathematics can be used.
The corresponding approximate Green’s function
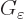

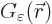 of the Poisson equation satisfies
of the Poisson equation satisfies
In the limit 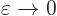 ,
, 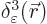 becomes the Dirac delta function
becomes the Dirac delta function 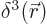 and
and
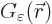 becomes the exact Green’s function
becomes the exact Green’s function
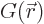 .
.
To find the approximate Green’s function, it will be assumed that
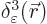 only depends on the distance
only depends on the distance 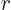

 from the origin. In other words, it is assumed to be
spherically symmetric. Then so is
from the origin. In other words, it is assumed to be
spherically symmetric. Then so is 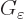 . (Note that
this assumption is not strictly necessary. That can be seen from the
general solution for the Poisson equation given earlier. But it
should at least be assumed that
. (Note that
this assumption is not strictly necessary. That can be seen from the
general solution for the Poisson equation given earlier. But it
should at least be assumed that 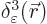 is
nonnegative. If it could have arbitrarily large negative values, then
is
nonnegative. If it could have arbitrarily large negative values, then
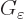 could be anything.)
could be anything.)
Now integrate both sides of the Poisson equation over a sphere of a
chosen radius 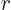 :
:
As noted, the delta function integrates to 1 as long as the vicinity
of the origin is included. That means that the right hand side is 1
as long as 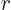
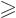
 . This will now be assumed.
The left hand side can be written out. That gives
. This will now be assumed.
The left hand side can be written out. That gives
According to the [divergence] [Gauss] [Ostrogradsky] theorem, the left
hand side can be written as a surface integral to give
Here 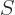 stands for the surface of the sphere of radius
stands for the surface of the sphere of radius 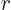 .
The total surface is
.
The total surface is 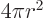 . Also
. Also 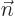 is the unit vector
orthogonal to the surface, in the outward direction. That is the
radial direction. The total differential of calculus then implies
that
is the unit vector
orthogonal to the surface, in the outward direction. That is the
radial direction. The total differential of calculus then implies
that  is the radial derivative
is the radial derivative
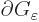

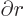 . So,
. So,
Because 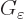 is required to vanish at large distances,
this integrates to
is required to vanish at large distances,
this integrates to
The exact Green’s function 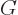 has
has  equal to zero, so
equal to zero, so
Finally the rigorous derivation without using poorly defined things
like delta functions. In the supposed general solution of the Poisson
equation given earlier, change integration variable to 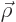

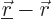
It is to be shown that the function 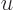 defined this way satisfies the
Poisson equation
defined this way satisfies the
Poisson equation 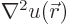

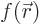 . To do so,
apply
. To do so,
apply  twice:
twice:
Here 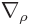 means differentiation with respect to the
components of
means differentiation with respect to the
components of 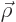 instead of the components of
instead of the components of 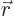 .
Because
.
Because  depends only on
depends only on 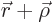 , you get the same
answer whichever way you differentiate.
, you get the same
answer whichever way you differentiate.
It will be assumed that the function  is well behaved, at least
continuous, and becomes zero reasonably quickly at infinity. In that
case, you can get a valid approximation to the integral above if you
exclude very small and very large values of
is well behaved, at least
continuous, and becomes zero reasonably quickly at infinity. In that
case, you can get a valid approximation to the integral above if you
exclude very small and very large values of 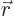 :
:
In particular, this approximation becomes exact in the limits where
the constants 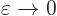 and
and 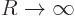 . The integral
can now be rewritten as
. The integral
can now be rewritten as
as can be verified by explicitly differentiating out the three terms
of the integrand. Next note that the third term is zero, because as
seen above 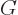 satisfies the homogeneous Poisson equation away from
the origin. And the other two terms can be written out using the
[divergence] [Gauss] [Ostrogradsky] theorem much like before. This
produces integrals over both the bounding sphere of radius
satisfies the homogeneous Poisson equation away from
the origin. And the other two terms can be written out using the
[divergence] [Gauss] [Ostrogradsky] theorem much like before. This
produces integrals over both the bounding sphere of radius 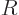 ,
as well as over the bounding sphere of radius
,
as well as over the bounding sphere of radius  .
But the integrals over the sphere of radius
.
But the integrals over the sphere of radius 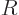 will be vanishingly
small if
will be vanishingly
small if  becomes zero sufficiently quickly at infinity.
Similarly, the integral of the first term over the small sphere is
vanishingly small, because
becomes zero sufficiently quickly at infinity.
Similarly, the integral of the first term over the small sphere is
vanishingly small, because 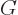 is 1
is 1
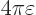 on the small
sphere but the surface of the small sphere is
on the small
sphere but the surface of the small sphere is
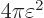 . However, in the second term, the
derivative of
. However, in the second term, the
derivative of 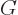 in the negative radial direction is
1/
in the negative radial direction is
1/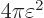 , which multiplies to 1 against the surface
of the small sphere. Therefore the second term produces the average
of
, which multiplies to 1 against the surface
of the small sphere. Therefore the second term produces the average
of 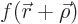 over the small sphere, and that becomes
over the small sphere, and that becomes 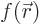 in the limit
in the limit 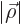

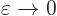 . So the
Poisson equation applies.
. So the
Poisson equation applies.
D.2.2 The screened Poisson equation
The so-called screened Poisson equation
is
Here  is supposed to be a given function and
is supposed to be a given function and 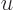 an unknown
function that is to be found. Further
an unknown
function that is to be found. Further 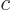 is a given constant. If
is a given constant. If
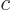 is zero, this is the Poisson equation. However, nonzero
is zero, this is the Poisson equation. However, nonzero 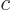 corresponds to the inhomogeneous steady Klein-Gordon equation for a
particle with nonzero mass.
corresponds to the inhomogeneous steady Klein-Gordon equation for a
particle with nonzero mass.
The analysis of the screened Poisson equation is almost the same as
for the Poisson equation given in the previous subsection. Therefore
only the differences will be noted here. The approximate Green’s
function must satisfy, away from the origin,
The solution to this that vanishes at infinity is of the form
where 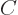 is some constant. To check this, plug it in, using the
expression (N.5) for
is some constant. To check this, plug it in, using the
expression (N.5) for  in spherical coordinates.
To identify the constant
in spherical coordinates.
To identify the constant 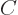 , integrate the full equation
, integrate the full equation
over a sphere of radius  around the origin and apply the
divergence theorem as in the previous subsection. Taking the limit
around the origin and apply the
divergence theorem as in the previous subsection. Taking the limit
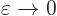 then gives
then gives 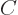
 1/
1/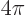 , which gives the
exact Green’s function as
, which gives the
exact Green’s function as
The rigorous derivation is the same as before save for an additional
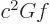 term in the integrand, which drops out against the
term in the integrand, which drops out against the
 one.
one.
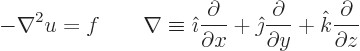
![]()
![]() .
.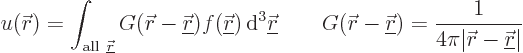
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
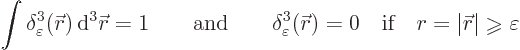
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() :
: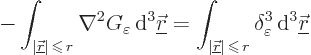
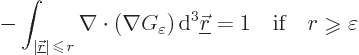
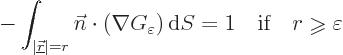
![]()
![]()
![]()
![]()
![]()
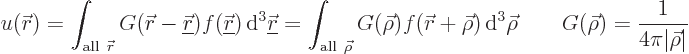
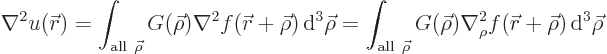
![]()
![]() :
: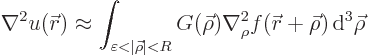
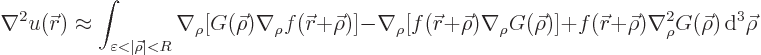
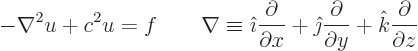
![]()
![]()