|
|
|
|
|
Next: A.42 Nuclear forces |
|
A very simple model can be used to give some context to the data of the deuteron. This addendum describes that model. Then it discusses the various major problems of the model. Some possible fixes for these problems are indicated.
In all cases it is assumed that the deuteron is modelled as a two-particle system, a proton and a neutron. Furthermore, the proton and neutron are assumed to have the same properties in the deuteron as they have in free space. These assumptions are not really true. For one, the proton and neutron are not elementary particles but combinations of quarks. However, ignoring that is a reasonable starting point in trying to understand the deuteron.
The deuteron contains two nucleons, a proton and a neutron. The
simple model assumes that the potential energy of the deuteron only
depends on the distance ![]()
![]()
![]()
![]()
![]() .
.![]() .
.
This model is analytically solvable. First, the deuteron involves the
motion of two particles, the proton and the neutron. However, the
problem may be simplified to that of an imaginary single
reduced mass
encircling the center of gravity of the
deuteron, addendum {A.5}.
The reduced mass in the simplified problem is half the mass of the
proton or neutron. (That ignores the tiny difference in mass between
the proton and neutron.) The potential for the reduced mass is ![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,10...
...ut(-50,70){\makebox(0,0)[lb]{$r^2\vert\psi\vert^2$}}
\end{picture}
\end{figure}](img5464.gif) |
The solution for the reduced mass problem may be worked out following
addendum {A.6}. Note that the model involves two
unknown parameters, the potential ![]()
![]() .
.
First of all, the binding energy should match the experimental 2.2247
MeV. Also, the root-mean square radial position of the nucleons away
from the center of the nucleus should be about 1.955 fm,
[J.P. McTavish 1982 J. Phys. G 8 911; J.L. Friar et al 1984
Phys. Rev. C 30 1084]. (Based on electron scattering experiments,
physicists are confident that the root-mean-square radial position of
the charge from the center of the deuteron is 2.14 fm. However, this
charge radius
is larger than the root mean square
radial position of the nucleons. The main reason is that the proton
has a finite size. For example, even in the hypothetical case that
the distance of the two nucleons from the center of gravity would be
zero, there would still be a positive charge radius; the one of the
proton. The proton by itself has a significant charge radius, 0.88
fm.) The distance ![]()
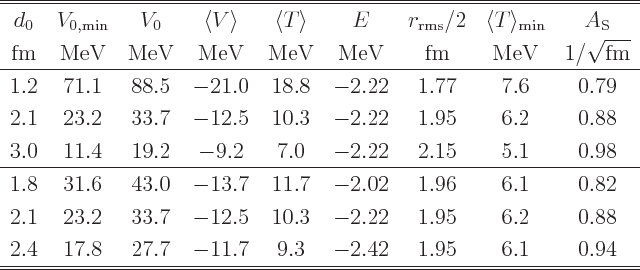 |
Table A.4 shows that these two experimental constraints are
met when the distance ![]()
![]()
![]()
There is some justification for this model. For one, it is well
established that the nuclear force very quickly becomes negligible
beyond some typical spacing between the nucleons. The above potential
reflects that. Based on better models, (in particular the so-called
OPEP potential), the typical range of the nuclear force is roughly 1.5
fm. The potential cut-off ![]()
The fact that both the model and exact potentials vanish at large
nucleon spacings also reflects in the wave function. It means that
the rate of decay of the wave function at large nucleon spacings is
correctly represented. The rate of decay depends only on the binding
energy ![]() .
.
To be more precise, the model wave function is, {A.6},
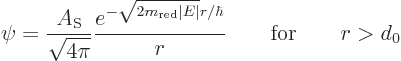
To be fair, this good agreement does not actually support the details
of the potential as much as it may seem. As the difference between
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
Another point in favor of the model is that the kinetic energy cannot be all wrong. In particular, the Heisenberg uncertainty relationship implies that the kinetic energy of the deuteron must be at least 6.2 MeV. The second-last column in the table shows the minimum kinetic energy that is possible for the root-mean-square radial nucleon position in the previous column. It follows that unavoidably the kinetic energy is significantly larger than the binding energy. That reflects the fact that the deuteron is only weakly bound. (For comparison, for the proton-electron hydrogen atom the kinetic energy and binding energy are equal.)
The model also supports the fact that there is only a single bound
state for the deuteron. The second column in the table gives the
smallest value of ![]()
![]()
![]()
A final redeeming feature of the model is that the deduced potential
![]()
While the model of the deuteron described in the previous subsection has
several redeeming features, it also has some major problems. The
problem to be addressed in this subsection is that the nuclear force
becomes repulsive when the nucleons try to get too close together. The
model does not reflect such a repulsive core
at all.
A simple fix is to declare nucleon spacings below a certain value
![]()
![]() .
.![]() ,
,![]() .
.
The modifications needed to the mathematics to include this repulsive
core are minor. Table A.5 summarizes the results. The
value of ![]()
Note that the value of the potential cut-off distance ![]()
![]() ,
,
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,13...
...ut(-50,70){\makebox(0,0)[lb]{$r^2\vert\psi\vert^2$}}
\end{picture}
\end{figure}](img5474.gif) |
Figure A.25 shows the potential and probability density.
The previous results without repulsive core are shown as thin grey
lines for easier comparison. Note that there are very distinctive
differences between the wave functions with and without repulsive
core. But astonishingly, the values for the root mean square nucleon
separation ![]()
![]()
Figure A.25 also shows corresponding results according to
the much more sophisticated Argonne ![]()
It is interesting to see from figure A.25 how small the 2.2 MeV binding energy of the deuteron really is, as compared to the minimum value of the potential energy.
An big problem with the model so far is that nucleon-nucleon interactions depend strongly on the nucleon spins. Such an effect also exists for the proton-electron hydrogen atom, {A.39.5}. However, there the effect is extremely small. For the deuteron, the effect of spin is dramatic.
The proton and neutron each have spin ![]() .
.
One simple way to fix this up is to write two different potentials.
One potential ![]()
![]()
That leaves only the problem of how to write the complete potential.
The complete potential should simplify to ![]()
![]()
![\begin{displaymath}
V = V_{\rm {t}}(r)
\left[\frac34+\frac{1}{\hbar^2}{\skew 6...
...c S}}_{\rm {p}}\cdot{\skew 6\widehat{\vec S}}_{\rm {n}}\right]
\end{displaymath}](img5480.gif) |
(A.258) |
So far it has been assumed that the potential in a given spin state
only depends on the distance ![]()
In terms of quantum mechanics, it gets phrased a little differently. A potential that only depends on the distance between the particles commutes with the orbital angular momentum operators. Then so does the Hamiltonian. And that means that the energy states can also be taken to be states of definite orbital angular momentum.
In particular, in the ground state, the proton and neutron should then be in a state of zero orbital angular momentum. Such a state is spherically symmetric. Therefore the proton charge distribution should be spherically symmetric too. All that would be just like for the electron in the hydrogen atom. See chapters 4.2, 4.3, 4.5, and 7.3, addendum {A.39}, and derivations {A.8} and {A.9} for more details on these issues.
However, the fact is that the charge distribution of the deuteron is
not quite spherically symmetric. Therefore, the potential cannot just
depend on the distance ![]()
![]()
The orientation of the chosen coordinate system should not make a
difference for the potential energy. From a classical point of view,
there are three nuclear angles that are nontrivial. The first two are
the angles that the vector ![]()
To check that, imagine a coordinate system with origin at the neutron.
Take the ![]() -
-![]() -
-![]() -
-![]() -
-
In quantum mechanics, angles involving angular momentum vectors are
not well defined. That is due to angular momentum uncertainty,
chapter 4.2. However, dot products between vectors can be
used to substitute for angles between vectors, for given lengths of
the vectors. Because the spin vectors have a given length, there are
four parameters that fix the geometry:
In order that orbital angular momentum is not conserved, the last two
parameters should be involved. But not separately, because they change
sign under a parity transformation or time reversal. It is known that
to very good approximation, nuclei respect the parity and
time-reversal symmetries. Terms quadratic in the last two parameters
are needed. And in particular, the product of the last two parameters
is needed. If you just square either parameter, you get a trivial
multiple of ![]() .
.
The bottom line is that the needed additional contribution to the
potential is due to the product of the final two terms. This
contribution is called the “tensor potential” for reasons that are not important. By
convention, the tensor potential is written in the form
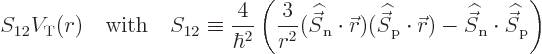 |
(A.259) |
It turns out that ![]()
![]()
![]()
![]()
![]()
It should also be noted that ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Figure A.26 illustrates the effects of the uncertainty in
orbital angular momentum on the deuteron. The data are taken from the
Argonne ![]()
The black curve is the probability density for finding the nucleons at
that spacing ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
That might suggest that the effect of the ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In terms of chapter 5.3, the lowering of the potential
energy is a twilight effect. Even for an ![]()
![]()
![]()
So far, the assumption has been that the potential of the deuteron only
depends on its geometry. But scattering data suggests that the
potential also depends on the motion of the nucleons. A similar effect,
the spin-orbit coupling
occurs for the proton-electron
hydrogen atom, addendum {A.39}. However, there the effect is
very small. Spin-orbit interaction is proportional to the dot product
of net orbital angular momentum and net nucleon spin. In particular, it
produces a term in the potential of the form