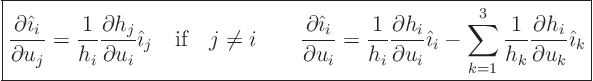|
|
|
|
|
Next: II. Linear Algebra |
|
Suppose that starting at Cartesian coordinates, we make a switch to new coordinates, like cylindrical or spherical ones? What is involved such a change in coordinates?
To find out, as always take the Cartesian coordinates ![]() to
form a vector
to
form a vector
parameter space. Note that that vector has no physical meaning; it is just a concise way of writing the three coordinates.
The Jacobian matrix
is
defined as the matrix of derivatives
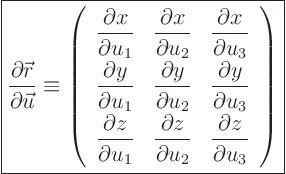
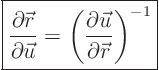
Any small change ![]() in the artificial vector
in the artificial vector ![]() corresponds to a small change in physical position
corresponds to a small change in physical position ![]() given by:
given by:
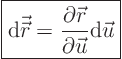
So the determinant of the Jacobian matrix is very important. This
determinant is called the Jacobian
![]() :
:
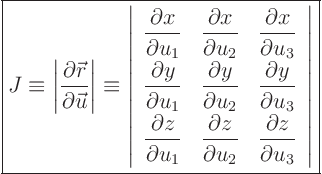
Now suppose you take a little block
![]() in the artificial parameter space. In
physical space, that little block will correspond to a little
parallelepiped with sides
in the artificial parameter space. In
physical space, that little block will correspond to a little
parallelepiped with sides
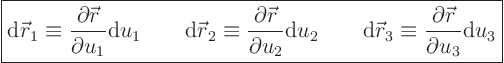
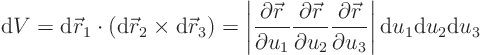
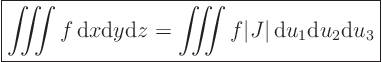
Orthogonal coordinates are a special case of the new coordinates
discussed in the previous subsection. For orthogonal coordinates, the
little parallelepiped in physical space corresponding to a little
block ![]() in coordinate space has orthogonal
sides. So it too is a little block, rather than just a little
parallelepiped.
in coordinate space has orthogonal
sides. So it too is a little block, rather than just a little
parallelepiped.
Since the three sides are proportional to the derivatives
![]() ,
, ![]() , and
, and
![]() , these derivatives must be orthogonal for
orthogonal coordinates. That means that if you write them as
magnitudes
, these derivatives must be orthogonal for
orthogonal coordinates. That means that if you write them as
magnitudes ![]() ,
, ![]() , and
, and ![]() times unit vectors
times unit vectors ![]() ,
,
![]() , and
, and ![]() ,
,
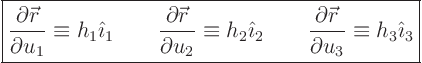
You can then convert the gradient, divergence, and curl operators to
the new coordinates. These formulas will involve the magnitudes,
called metric indices
![]() ,
, ![]() , and
, and ![]() . Since
you can find these formulae in any mathematical handbook, they will
not be discussed here.
. Since
you can find these formulae in any mathematical handbook, they will
not be discussed here.
But often you want to find other derivatives in the new coordinates.
To do so, you must know how to find the derivatives of the unit
vectors ![]() ,
, ![]() , and
, and ![]() . These formulae are not
soeasy to find, so they will be given here. For any
. These formulae are not
soeasy to find, so they will be given here. For any ![]() equal to 1,
2, or 3, and any
equal to 1,
2, or 3, and any ![]() equal to 1, 2, or 3,
equal to 1, 2, or 3,