| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
Subsections
18.1 Basic Concepts
18.1.1 The prevalence of partial differential equations
Partial differential equations are equations involving derivatives
with respect to more than one independent variable.
Partial differential equations are the basic equations in many areas
of science and engineering. Some examples:
- Fluid mechanics
- The basic equations that govern the inviscid
flow of simple idealized substances are called the Euler equations.
The basic equations that govern the viscous flow of simple
substances like air and water under normal conditions are called the
Navier-Stokes equations. Both are partial differential equations.
Nonlinear ones, unfortunately. However, they do become linear in
many special cases of great interest.
- Heat transfer
- The equations of heat conduction and convection
are partial differential equations. Radiation may be described by
Maxwell’s equations, which are also partial differential
equations. However, often radiation can be more simply described by
so-called boundary integral methods. In the most basic cases, the
partial differential equations describing convection are linear.
- Solid mechanics
- The equations that govern simple solids are
partial differential equations. Often the interest is in steady
problems. The equations for simple relatively stiff solids are
linear.
- Dynamics
- The dynamics of flexible solids is governed by
partial differential equations. The equations for simple relatively
stiff solids are linear.
- Electromagnetics and optics
- The Maxwell equations that govern
basic electromagnetic phenomena are partial differential equations.
They are linear in vacuum. Simplified partial differential
equations govern the special cases of electrostatics and
magnetostatics.
- Geometry
- Many geometrical issues such as minimal surfaces and
developable surfaces are governed by partial differential equations.
The equation for minimal surfaces may be reduced to a very simple
linear one.
That did not even touch on such areas as biology and economics that
are also awash in partial differential equations.
18.1.2 Definitions
Here is a list of some basic definitions used for partial differential
equations:
- Partial differential equations
- are equations that involve
derivatives with respect to more than one independent variable. The
simplest partial differential equation that you can write is:
In that case 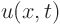 would be unknown, or dependent variable. That
is the function you want to find. The independent variables would
be
would be unknown, or dependent variable. That
is the function you want to find. The independent variables would
be 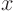 and
and 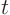 . People usually think of a spatial coordinate when
they use
. People usually think of a spatial coordinate when
they use 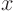 , and time when they use
, and time when they use 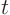 .
.
It may be noted that equations that involve only derivatives with
respect to one independent variable are called “ordinary
differential equations.” Equations that also involve
integrals are called integro-differential equations.
- Partial derivatives
- are derivatives with respect to one
independent variable, keeping the other variables constant. The
figure below illustrates the definition of partial derivatives:
A simple numerical approximation of a partial derivative will just
eliminate the limit process. In that case 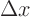 and
and
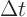 are merely taken to be small compared to the typical
scale of the problem.
are merely taken to be small compared to the typical
scale of the problem.
- Order
- The order of a partial differential equation is
the order of the highest derivative. Generally speaking,
the highest derivatives are most responsible for the nature
of the solutions.
- Degree
- The degree of a partial differential equation is the
highest power to which the dependent variable appears in the
equation.
Consider for example the Burgers’ equation
It is the simplest nonlinear model for the equations of fluid
mechanics, and for other systems involving shock formation. It is
of order 1 and degree 2.
- Linear
- partial differential equations are equations of first
degree. The terms that are of the first degree in the unknown are
called the homogeneous part. The remaining terms that do not
involve the unknown are called the inhomogeneous part.
Consider the following Poisson equation governing steady heat
conduction in a plate with external heat addition:
Here  is the temperature,
is the temperature, 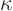 the heat conduction
coefficient, and the right hand side represents the external heat
added per unit area. This equation is first degree (in
the heat conduction
coefficient, and the right hand side represents the external heat
added per unit area. This equation is first degree (in  .) The
left hand side, linear in
.) The
left hand side, linear in  is the homogeneous part and the right
hand side, independent of
is the homogeneous part and the right
hand side, independent of  , is the inhomogenous part.
, is the inhomogenous part.
The following equation describes steady heat conduction in a plate
without external heat addition, but with a heat conduction coefficient
that depends on temperature:
This equation is nonlinear. It is of infinite degree, not second
degree, because the Taylor series of 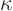 intruduces all powers
of
intruduces all powers
of  . However, this equation is still linear in terms of the
highest, second order, derivatives
. However, this equation is still linear in terms of the
highest, second order, derivatives 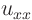 and
and 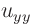 . (Not
counting lower order derivatives.) Therefore it is called
. (Not
counting lower order derivatives.) Therefore it is called
quasi-linear.
- The domain
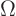
- is usually taken to be the spatial region
in which the partial differential equation applies. For unsteady
heat conduction in a sphere, the domain
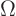 is the sphere and
time is an additional coordinate.
is the sphere and
time is an additional coordinate.
- The boundary
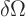
- is where the domain stops.
Boundary points are immediately adjacent to both points inside the
domain and points outside it. The boundary is also often indicated
by
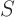 (for surface). Typically,
(for surface). Typically, 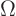 indicates the domain
without the boundary points and
indicates the domain
without the boundary points and 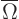 the domain
including the boundary points.
the domain
including the boundary points.
For unsteady heat conduction in a sphere of radius 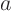 , the boundary
is all points with spherical coordinate
, the boundary
is all points with spherical coordinate 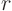 equal to
equal to 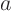 . It is the
surface of the sphere. For this example
. It is the
surface of the sphere. For this example 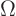 is all points
is all points
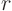
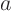 and
and 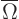 is all points
is all points 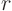
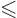
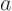 .
.
- Boundary conditions
- are conditions on the solution that apply at
points on the boundary.
- Initial conditions
- are conditions on the solution that apply at
the starting time. Almost always, the starting time is taken to be
the zero of time.
- Singularities
- You cannot do much in partial differential
equations without having to deal with singularities. There might be
singularities in the solution, in the initial and boundary
conditions, or in the shape of the boundary. Some typical
singularities, in a rough order from relatively mild to more severe,
are
- Locations where all derivatives exist, but the function does
not have a Taylor series with a nonzero radius of convergence.
For example, that happens for the function
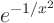 at
at 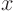
 0.
0.
- Locations where higher order derivatives have singularities.
For example, the function
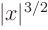 has an infinite second order
derivative at
has an infinite second order
derivative at 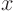 =0. That means it has infinite radius of
curvature at
=0. That means it has infinite radius of
curvature at 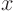
 0. In general, the lower the order of the
derivative involved, the stronger the singularity.
0. In general, the lower the order of the
derivative involved, the stronger the singularity.
- Kinks: Locations where the first derivative jumps from
one finite value to another. For example, the function
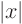

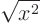 has a kink at
has a kink at 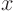
 0.
0.
- Cusps: where the function itself is still continuous,
but the derivative jumps from
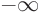 to
to 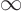 or vice-versa.
For example,
or vice-versa.
For example, ![$\sqrt[3]{x^2}$](img650.gif) has a cusp at
has a cusp at 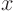
 0
0
- Jumps: where the function jumps from one finite value to
another. For example, the Heaviside function
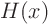 , which is 0
for negative
, which is 0
for negative 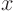 and 1 for positive
and 1 for positive 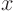 , has a jump at
, has a jump at 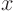
 0.
0.
- Spikes: where the function is infinite at a single
point. An important example is the Dirac delta function
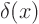 , which is the derivative of the Heaviside function.
The delta function is a single infinite spike at
, which is the derivative of the Heaviside function.
The delta function is a single infinite spike at 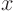
 0 and the
area under the spike is 1. If you take derivatives of the delta
function, you get increasingly singular functions. For example,
the first derivative is the more singular
0 and the
area under the spike is 1. If you take derivatives of the delta
function, you get increasingly singular functions. For example,
the first derivative is the more singular dipole.
- Poles: where the function goes to infinity. For
example, the function
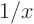 has a
has a simple pole
at
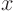
 0. The higher the negative power of
0. The higher the negative power of 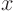 , the more singular
the function. For example
, the more singular
the function. For example 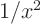 is more singular than
is more singular than 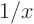 .
.
18.1.3 Typical boundary conditions
To get a meaningful solution to a partial differential equation, you
will need initial and/or boundary conditions. Initial conditions
are normally straightforward. Boundary conditions vary a lot,
however.
There are some very simple types of boundary condition that you must
know by heart:
- Dirichlet
- The value of the unknown
 itself is given on the
boundary:
itself is given on the
boundary:
Here 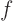 is some given function of the position on the surface.
is some given function of the position on the surface.
- Neumann
- The derivative
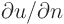 of the unknown
in the direction normal to the boundary is given. Here
of the unknown
in the direction normal to the boundary is given. Here 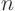 is the
coordinate normal to the boundary:
is the
coordinate normal to the boundary:
If the boundary is oblique, the following formula can be used to
relate the derivative in the direction normal to the boundary to the
partial derivatives of  in Cartesian coordinates:
in Cartesian coordinates:
Here 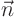 is a unit vector that is normal to the boundary at
the considered point.
is a unit vector that is normal to the boundary at
the considered point.
Note that if  itself is prescribed on the boundary, it already
implies the value of derivative along the boundary. That is
why only the derivative normal to the boundary is included in this
list of the most basic boundary conditions.
itself is prescribed on the boundary, it already
implies the value of derivative along the boundary. That is
why only the derivative normal to the boundary is included in this
list of the most basic boundary conditions.
- Mixed
- A linear combination of
 and
and 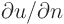 is given on the boundary. This is also called a
is given on the boundary. This is also called a
radiation” or “Robin
boundary
condition.
Here 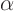 ,
, 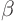 , and
, and 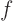 are all given functions of the
position on the surface. Such boundary conditions are often used in
simple wave propagation problems to indicate that no waves enter the
domain from outside.
are all given functions of the
position on the surface. Such boundary conditions are often used in
simple wave propagation problems to indicate that no waves enter the
domain from outside.
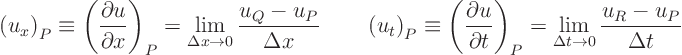
![\begin{figure}
\begin{center}
\leavevmode
\setlength{\unitlength}{1pt}
...
... \put(-82,70){\makebox(0,0)[r]{$t$}}
\end{picture}
\end{center}
\end{figure}](img632.gif)
![]() and
and
![]() are merely taken to be small compared to the typical
scale of the problem.
are merely taken to be small compared to the typical
scale of the problem.
![]() , the boundary
is all points with spherical coordinate
, the boundary
is all points with spherical coordinate ![]() equal to
equal to ![]() . It is the
surface of the sphere. For this example
. It is the
surface of the sphere. For this example ![]() is all points
is all points
![]()
![]()
![]() and
and ![]() is all points
is all points ![]()
![]()
![]() .
.
![]() in Cartesian coordinates:
in Cartesian coordinates:
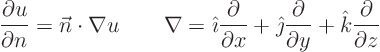
![]() itself is prescribed on the boundary, it already
implies the value of derivative along the boundary. That is
why only the derivative normal to the boundary is included in this
list of the most basic boundary conditions.
itself is prescribed on the boundary, it already
implies the value of derivative along the boundary. That is
why only the derivative normal to the boundary is included in this
list of the most basic boundary conditions.