|
|
|
|
|
Next: 18.3 Properly Posedness |
|
There are a few standard examples of partial differential equations. You must know these by heart.
The Laplace equation governs basic steady heat conduction, among much else.
An example problem is shown in figure 18.1. Physically it
is steady heat conduction in a rectangular plate of dimensions
![]() . The unknown
. The unknown ![]() in this example is the temperature.
The independent variables are the Cartesian coordinates
in this example is the temperature.
The independent variables are the Cartesian coordinates ![]() and
and
![]() . The domain
. The domain ![]() is the two-dimensional interior of the plate.
The boundary
is the two-dimensional interior of the plate.
The boundary ![]() is the one-dimensional perimeter of the
plate. (The boundary might still be indicated by
is the one-dimensional perimeter of the
plate. (The boundary might still be indicated by ![]() instead of
instead of
![]() even though here it is not a surface.)
even though here it is not a surface.)
The Laplace equation also describes ideal flows, unidirectional flows, membranes, electrostatics and magnetostatics, complex functions, and countless other problems.
In any number of dimensions, the Laplace equation reads
Some important properties of the Laplace equation are:
boundary-value problems.At every point on the boundary, one boundary condition should be prescribed. For example, consider the example problem figure 18.1. On the vertical boundaries, the temperature is given. That is a Dirichlet boundary condition. On the horizontal boundaries, the heat flow out of the boundary is given. Now the heat flow is proportional to the gradient of the temperature. In particular, the heat flow in the vertical direction is proportional to
(For domains that extent to infinity, various rules above assume that you consider the infinite domain as the limit of a finite one.)
The Laplace equation is the basic example of what is called an
elliptic
partial differential equation. Solutions of
the Laplace equation are called harmonic functions.
Derive the Laplace equation for steady heat conduction in a two-dimensional plate of constant thickness ![]() . Do so by considering a little Cartesian rectangle of dimensions
. Do so by considering a little Cartesian rectangle of dimensions ![]() . A sketch is shown below:
. A sketch is shown below:
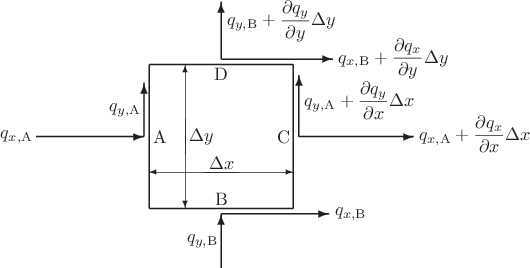
Assume Fourier’s law:
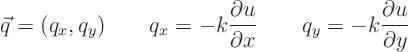
If you want the heat flow ![]() through an area element
through an area element ![]() that is not normal to the direction of heat flow, the expression is
that is not normal to the direction of heat flow, the expression is
Assume that no heat is added to the little rectangle from external sources.
Derive the Laplace equation for steady heat conduction using vector analysis. Assume Fourier’s law as given in the previous question. In vector form
Assume that no heat is added to the solid from external sources.
Consider the Laplace equation within a unit circle:
To find the value of ![]() at the point (0.1,0.2), can I just plug in the coordinates of that point into the boundary condition? If not, what is the correct value of u at the point, and what would I get from the boundary condition?
at the point (0.1,0.2), can I just plug in the coordinates of that point into the boundary condition? If not, what is the correct value of u at the point, and what would I get from the boundary condition?
Also answer the above questions for the following problem:
Suppose you have a Laplace equation problem where the boundary is symmetric around the ![]() -axis, like, say, in the previous two problems. In general, such a symmetric boundary means that if
-axis, like, say, in the previous two problems. In general, such a symmetric boundary means that if ![]() is a boundary point, then so is
is a boundary point, then so is ![]() . Also assume that
. Also assume that ![]() is given as an antisymmetric function of x on this boundary;
is given as an antisymmetric function of x on this boundary; ![]()
![]()
![]() for any boundary point. Show that in that case,
for any boundary point. Show that in that case, ![]() is antisymmetric function of
is antisymmetric function of ![]() everywhere, i.e.
everywhere, i.e. ![]()
![]()
![]() everywhere.
everywhere.
Then show that this means that the solution ![]() will be zero on the
will be zero on the ![]() axis.
axis.
Also explain why the above would no longer be true if you had a first order ![]() derivative in the PDE, like for example
derivative in the PDE, like for example ![]()
![]() 0.
0.
Consider the Laplace equation within a unit circle, but now in polar coordinates:
The solution is the Poisson integral formula
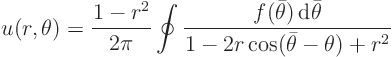
Now suppose that function ![]() is increased slightly, by an amount
is increased slightly, by an amount ![]() , and only in a very small interval
, and only in a very small interval ![]()
![]()
![]()
![]()
![]() .
.
Does the solution ![]() change everywhere in the circle, or only in the immediate vicinity of the interval on the boundary at which
change everywhere in the circle, or only in the immediate vicinity of the interval on the boundary at which ![]() was changed. What is the sign of the change in
was changed. What is the sign of the change in ![]() if
if ![]() is positive?
is positive?
Consider the following Laplace equation problem in a unit square:
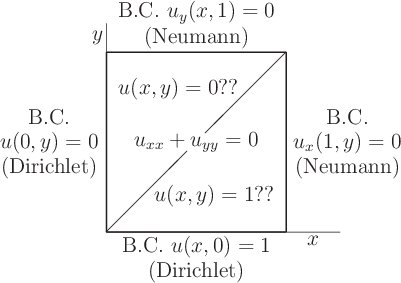
The problem as shown has a unique solution. It is relevant to a case of heat conduction in a square plate, with ![]() the temperature. Someone proposed that the solution should be simple: in the upper triangle the solution
the temperature. Someone proposed that the solution should be simple: in the upper triangle the solution ![]() is 0, and in the lower triangle, it is 1.
is 0, and in the lower triangle, it is 1.
Thoroughly discuss this proposed solution. Determine whether the boundary conditions and initial conditions are satisfied. Is the partial differential equation satisfied in both triangles?
Explain why all isotherms except 0 and 1 coincide with the 45![]() line. And why the zero and 1 isotherms are indeterminate.
line. And why the zero and 1 isotherms are indeterminate.
Finally discuss whether the solution is right.
If for the problem of the previous question, the proposed solution is wrong, then so are the described isotherms.
To get a clue about the correct solution and isotherms, consider the following simpler problem. In this problem the top and right boundaries have been distorted into a quarter circle:
Also neatly draw ![]() versus the polar angle
versus the polar angle ![]() at
at ![]()
![]() 0.5. In a separate graph, draw the solution proposed in the previous section,
0.5. In a separate graph, draw the solution proposed in the previous section, ![]()
![]() 1 for
1 for ![]()
![]()
![]() and
and ![]()
![]() 0 for
0 for ![]()
![]()
![]() , again against
, again against ![]() at
at ![]()
![]() 0.5.
0.5.
Now go back to the problem of the previous question and very neatly sketch the correct ![]()
![]() 0, 0.25, 0.5, 0.75, and 1 isotherms for that problem. Pay particular attention to where the 0.25, 0.5, and 0.75 isotherms meet the boundaries and under what angle.
0, 0.25, 0.5, 0.75, and 1 isotherms for that problem. Pay particular attention to where the 0.25, 0.5, and 0.75 isotherms meet the boundaries and under what angle.
Return once again to the problem of the second-last question.
The correct solution to this problem, that you would find using the so-called method of separation of variables, is:
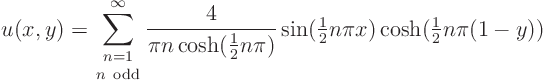
Now shed some light on the question why this solution is smooth for any arbitrary ![]()
![]() 0. To do so, first explain why any sum of sines of the form
0. To do so, first explain why any sum of sines of the form
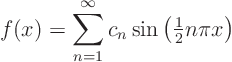
Next, you are allowed to make use of the fact that the function is still smooth if the coefficients ![]() go to zero quickly enough. In particular, if you can show that
go to zero quickly enough. In particular, if you can show that
Use this to show that ![]() above is indeed infinitely smooth for any
above is indeed infinitely smooth for any ![]()
![]() 0. And show that it is not true for
0. And show that it is not true for ![]()
![]() 0, where the solution jumps at the origin.
0, where the solution jumps at the origin.
The heat equation governs basic unsteady heat conduction, among much else.
An example problem is shown in figure 18.2. Physically it
is unsteady heat conduction in a bar of length ![]() . The unknown
. The unknown
![]() is the temperature. The independent variables in this case are
the coordinate
is the temperature. The independent variables in this case are
the coordinate ![]() along the bar and the time
along the bar and the time ![]() . The domain
. The domain
![]() in this example is the bar. Mathematically, that is the line
segment 0
in this example is the bar. Mathematically, that is the line
segment 0 ![]()
![]()
![]()
![]() with
with ![]() the length of the bar. The
boundary
the length of the bar. The
boundary ![]() consists in this case of a mere two points:
consists in this case of a mere two points:
![]()
![]() 0 and
0 and ![]()
![]()
![]() .
.
The heat equation also describes unsteady viscous unidirectional flows and many other diffusive phenomena.
In any number of dimensions, the heat equation reads
Some important properties of the heat equation are:
The heat equation is the basic example of what is called a
parabolic
partial differential equation.
This is a continuation of a corresponding question in the subsection on the Laplace equation. See there for a definition of terms.
Derive the heat equation for unsteady heat conduction in a two-dimensional plate of thickness ![]() , Do so by considering a little Cartesian rectangle of dimensions
, Do so by considering a little Cartesian rectangle of dimensions ![]() .
.
In particular, derive the heat conduction coefficient ![]() in terms of the material heat coefficient
in terms of the material heat coefficient ![]() , the plate thickness
, the plate thickness ![]() , and the specific heat of the solid
, and the specific heat of the solid ![]() .
.
This is a continuation of a corresponding question in the subsection on the Laplace equation. See there for a definition of terms.
Derive the heat equation for unsteady heat conduction using vector analysis.
This equation governs basic vibrations, among much else.
An example problem, vibrations of a string, is shown in figure
18.3. The unknown ![]() is the transverse deflection of the
string. The independent variables are again
is the transverse deflection of the
string. The independent variables are again ![]() and
and ![]() like for the
heat equation example. The domain
like for the
heat equation example. The domain ![]() is again the
is again the ![]() -interval
along the string and the boundary
-interval
along the string and the boundary ![]() is the two end
points.
is the two end
points.
The heat equation also describes acoustics, steady supersonic flow, water waves, optics, electromagnetic waves, and many other basic phenomena characterized by wave propagation.
In any number of dimensions, the wave equation reads
Some important properties of the wave equation are:
The wave equation is the basic example of what is called a
hyperbolic
partial differential equation.
Derive the wave equation for small transverse vibrations of a string by considering a little string segment of length ![]() .
.
Maxwell’s equations for the electromagnetic field in vacuum are
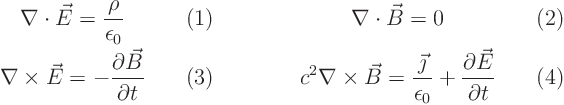
Show that if you know how to solve the standard wave equation, you know how to solve Maxwell’s equations. At least, if the charge and current densities are known.
Identify the wave speed.
Consider the following wave equation problem in a unit square:
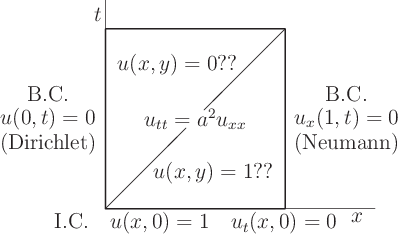
This is basically identical to a Laplace equation problem in the first subsection. Like that problem, the above wave equation problem has a unique solution. It is relevant to a case of acoustics in a tube, with ![]() the pressure. Someone proposed that the solution should be simple: in the upper triangle the solution
the pressure. Someone proposed that the solution should be simple: in the upper triangle the solution ![]() is 0, and in the lower triangle, it is 1.
is 0, and in the lower triangle, it is 1.
Thoroughly discuss this proposed solution. Determine whether the boundary conditions and initial conditions are satisfied. Is the partial differential equation satisfied in both triangles? Finally discuss whether the solution is right. Consider the value of the wave speed ![]() in your answer.
in your answer.
Sketch the isobars of the correct solution. In particular, sketch the ![]()
![]() 0 0.25, 0.5, 0.75, and 1 isobars, if possible. Sketch both the case that
0 0.25, 0.5, 0.75, and 1 isobars, if possible. Sketch both the case that ![]()
![]() 1 and that
1 and that ![]()
![]()
![]() .
.
Return again to the problem of the last question. Assume ![]()
![]() 1.
1.
The correct solution to this problem, that you would find using the so-called method of separation of variables, is:
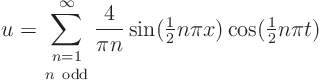
Explain that it produces the moving jump in the solution as given in the previous question.
The discontinuous solution given in the previous question is right in this case. It is right because it is the proper limiting case of a smooth solution that everywhere satisfies the partial differential equation. In particular, if you sum the above sum for ![]() up to a very high, but not infinite value of
up to a very high, but not infinite value of ![]() , you get a smooth solution of the partial differential equation that satisfies all initial and boundary conditions, except that the value of
, you get a smooth solution of the partial differential equation that satisfies all initial and boundary conditions, except that the value of ![]() at
at ![]()
![]() 0 still shows small deviations from
0 still shows small deviations from ![]()
![]() 1. The more terms you sum, the smaller those deviations become. (There will always be some differences right at the singularity, but these will be restricted to a negligibly small vicinity of
1. The more terms you sum, the smaller those deviations become. (There will always be some differences right at the singularity, but these will be restricted to a negligibly small vicinity of ![]()
![]() 0.)
0.)
Find the possible plane wave solutions for the two-dimensional wave equation
Also find the possible standing wave solutions. Assume homogeneous Dirichlet or Neumann boundary conditions on some rectangle 0 ![]()
![]()
![]()
![]() , 0
, 0 ![]()
![]()
![]()
![]() . What is the frequency?
. What is the frequency?
Repeat for the generalized equation