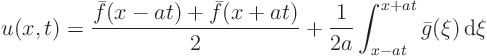22.2 Comparison with D'Alembert

The example problem of the previous section was also solved in chapter 21 using D'Alembert. It is interesting to compare the two solutions.

The separation of variables solution took the form:

$$u = \sum_{n=1}^\infty \left[ f_n \cos\frac{(2n-1)\pi... ...2n-1)\pi at}{2\ell} \right] \cos\frac{(2n-1)\pi x}{2\ell}$$

Some of its nice features are:

• It shows the natural frequencies (tones) to be $\pi a/2\ell$, $3 \pi a/2\ell$,...
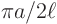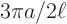• It shows the energy, so the strength, of each harmonic.
• The method is not restricted to the one-di­men­sion­al wave equation.

The D’Alembert solution took the form

$$u(x,t) = \frac{\bar f(x-at) + \bar f(x+at)}{2} + \frac{1}{2a} \int_{x-at}^{x+at} \bar g(\xi) { \rm d}\xi$$

Some of its nice features are

• The pressure can be evaluated at any point without doing infinite sums.
• It shows how wave fronts propagate.
• It shows regions of influence and dependence.

In short, each method has its advantages and disadvantages.