|
|
|
|
|
Next: 22.2 Comparison with D'Alembert |
|
The method of separation of variables shall first be demonstrated for a simple example. The method as described here will work as long as the spatial region is finite and has homogeneous boundary conditions.
The problem is to find the unsteady pressure field ![]() in a pipe
with one end closed and the other open to the atmosphere:
in a pipe
with one end closed and the other open to the atmosphere:
We will try to find a solution of this problem in the form
There are two big reasons why the ![]() must be the eigenfunctions,
rather than the
must be the eigenfunctions,
rather than the ![]() :
:
(If the spatial range is infinite or semi-infinite, you may be able to use a Fourier transform. Alternatively, you may be able to use a Laplace transform in time.)
The first step is to find the eigenfunctions ![]() .
.
The eigenfunctions are found from requiring that each individual term of the formis capable of satisfying the homogeneous partial differential equation and the homogeneous boundary conditions.
In this particular example the partial differential equation is
homogeneous. But even if it is not, i.e. if the partial differential
equation was something like
By convention, ![]() is usually written as
is usually written as ![]() and
and ![]() as
as
![]() in this step. To see when
in this step. To see when ![]() satisfies the homogeneous
partial differential equation, plug it in:
satisfies the homogeneous
partial differential equation, plug it in:
The trick is now to take the terms containing time to one side of the
equation and the terms containing ![]() to the other side.
to the other side.
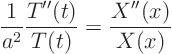
While the right hand side, ![]() , does not depend on
, does not depend on ![]() , you
would think that it would depend on the position
, you
would think that it would depend on the position ![]() ; both
; both ![]() and
and
![]() change when
change when ![]() changes. But actually,
changes. But actually, ![]() does not
change with
does not
change with ![]() ; after all, if we change
; after all, if we change ![]() , it does nothing to
, it does nothing to ![]() ,
so the left hand side does not change. And since the right hand side
is the same, it too does not change. So the right hand side does not
depend on either
,
so the left hand side does not change. And since the right hand side
is the same, it too does not change. So the right hand side does not
depend on either ![]() or
or ![]() ; it must be a constant. By convention, we
call the constant
; it must be a constant. By convention, we
call the constant ![]() :
:
If we also require ![]() to satisfy the same homogeneous boundary
conditions as
to satisfy the same homogeneous boundary
conditions as ![]() . In this case, that means that at
. In this case, that means that at ![]()
![]() 0, its
0, its
![]() -derivative is zero, and that at
-derivative is zero, and that at ![]()
![]()
![]() ,
, ![]() itself is zero. So
we get the following problem for
itself is zero. So
we get the following problem for ![]() :
:
Note that the problem is completely homogeneous: ![]()
![]() 0 satisfies
both the partial differential equation and the boundary
conditions. This is similar to the eigenvalue problem for vectors
0 satisfies
both the partial differential equation and the boundary
conditions. This is similar to the eigenvalue problem for vectors
![]()
![]()
![]() , which is certainly always true when
, which is certainly always true when ![]() . But for the eigenvalue problem, we are interested in
nonzero vectors
. But for the eigenvalue problem, we are interested in
nonzero vectors ![]() for which
for which ![]()
![]()
![]() . That
only occurs for special values
. That
only occurs for special values ![]() ,
, ![]() , ...of
, ...of
![]() .
.
Similarly, we are interested only in nonzero solutions X(x) of the
above ordinary differential equation and boundary conditions.
Eigenvalue problems for functions such as the one above are called
Sturm-Liouville problems.
The biggest differences from
matrix eigenvalue problems are:
Fortunately, the above ordinary differential equation is simple: it is
a constant coefficient one, so we write its characteristic polynomial:
Since ![]()
![]()
![]()
We try to satisfy the boundary conditions:
Since ![]()
![]()
![]()
![]() 0 we have a multiple root of the characteristic
equation, and the solution is
0 we have a multiple root of the characteristic
equation, and the solution is
We try to satisfy the boundary conditions again:
Since ![]()
![]()
![]()
![]()
![]() , the solution of the ordinary differential equation
is after cleanup:
, the solution of the ordinary differential equation
is after cleanup:
We try to satisfy the first boundary condition:
We now try to also satisfy the second boundary condition:
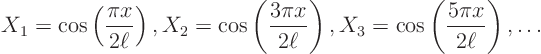
The eigenvalues and eigenfunctions have been found. If we want to
evaluate them on a computer, we need a general formula for them. You
can check that it is:
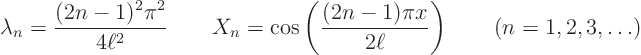
If you look back to the beginning of the previous subsection, you may
wonder about the function ![]() . It satisfied
. It satisfied
However, it is far more straightforward not to do so. Now that the
eigenfunctions ![]() have been found, the general expression for the
solution,
have been found, the general expression for the
solution,
However, most people do solve for the ![]() corresponding to each
eigenvalue
corresponding to each
eigenvalue ![]() . If you want to follow the crowd, please keep
in mind the following:
. If you want to follow the crowd, please keep
in mind the following:
Now that the eigenfunctions are known, the problem may be solved. To do so, everything needs to be written in terms of the eigenfunctions. And that means everything, including the partial differential equation and the initial conditions.
We first write our solution ![]() in terms of the eigenfunctions:
in terms of the eigenfunctions:
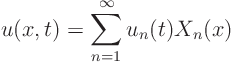
Fourier seriesfor
We know our eigenfunctions ![]() , but not yet our Fourier
coefficients
, but not yet our Fourier
coefficients ![]() . In fact, the
. In fact, the ![]() are what is still
missing; if we know the
are what is still
missing; if we know the ![]() , we can find the solution
, we can find the solution ![]() that we
want by doing the sum above. On a computer probably, if we want to
get high accuracy. Or just the first few terms by hand, if we accept
some numerical error.
that we
want by doing the sum above. On a computer probably, if we want to
get high accuracy. Or just the first few terms by hand, if we accept
some numerical error.
Next we write the complete partial differential equation, ![]() , in terms of the eigenfunctions:
, in terms of the eigenfunctions:
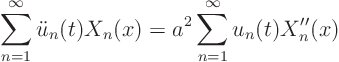
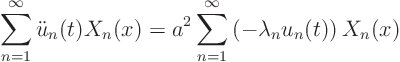
The above ordinary differential equations can be solved easily. For
each value of ![]() it is a constant coefficient equation. So you write
the characteristic equation
it is a constant coefficient equation. So you write
the characteristic equation ![]()
![]()
![]() . That give
. That give
![]()
![]()
![]() . Then the solution is
. Then the solution is
So, we have already found our pressure a bit more precisely:
![\begin{displaymath}
u(x,t)= \sum_{n=1}^\infty
\left[
D_{1n} \cos\left(a \s...
...
D_{2n} \sin\left(a \sqrt\lambda_n t\right)
\right] X_n(x)
\end{displaymath}](img1444.gif)
To do so, we also write the initial condition ![]()
![]()
![]() and
and
![]()
![]()
![]() in terms of the eigenfunctions:
in terms of the eigenfunctions:
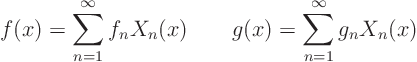
Using the Fourier series for ![]() ,
, ![]() , and
, and ![]() above, the two initial
conditions become
above, the two initial
conditions become
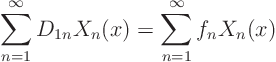
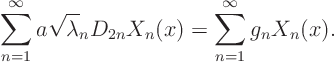
The Fourier series for ![]() becomes now
becomes now
![\begin{displaymath}
u(x,t)= \sum_{n=1}^\infty
\left[
f_n \cos\left(a \sqrt...
...ambda_n} \sin\left(a \sqrt\lambda_n t\right)
\right] X_n(x)
\end{displaymath}](img1453.gif)
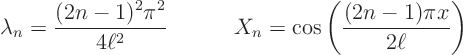
Now ![]() and
and ![]() are, supposedly, given functions, but how do we
find their Fourier coefficients? The answer is the following important
formula:
are, supposedly, given functions, but how do we
find their Fourier coefficients? The answer is the following important
formula:
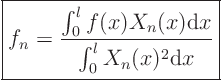
orthogonality relation. Even if
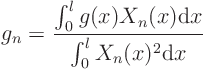
We are done! Or at least, we have done as much as we can do until
someone tells us the actual functions ![]() and
and ![]() . If they do,
we just do the integrals above to find all the
. If they do,
we just do the integrals above to find all the ![]() and
and ![]() , (maybe
analytically or on a computer), and then we can sum the expression for
, (maybe
analytically or on a computer), and then we can sum the expression for
![]() for any
for any ![]() and
and ![]() that strikes our fancy.
that strikes our fancy.
Note that we did not have to do anything with the boundary conditions
![]()
![]() 0 and
0 and ![]()
![]() 0. Since every eigenfunction
0. Since every eigenfunction ![]() satisfies them, the expression for
satisfies them, the expression for ![]() above automatically also
satisfies these homogeneous boundary conditions.
above automatically also
satisfies these homogeneous boundary conditions.