|
|
|
|
|
Next: 18.5 Variational methods [None] |
|
Energy methods derive some sort of system energy
from
a partial differential equation. That energy may then be used to
derive such things as existence and/or uniqueness of the solution,
and whether it depends continuously on the data.
Consider the following very general Poisson equation problem:
The objective in this subsection is to show that solutions to this
problem are unique as long as ![]() and
and ![]() do not have opposite sign.
Assuming that the problem has a solution in the first place, there is
only one.
do not have opposite sign.
Assuming that the problem has a solution in the first place, there is
only one.
To prove that, it must be proved that any two solutions ![]() and
and
![]() of the same problem cannot be different. That they must be the
same. In other words, it must be proved that the difference
of the same problem cannot be different. That they must be the
same. In other words, it must be proved that the difference
![]()
![]()
![]() between any two solutions
between any two solutions ![]() and
and ![]() is zero.
is zero.
The proof starts with deriving the equations satisfied by the
difference ![]() . Since by assumption
. Since by assumption ![]() and
and ![]() are both
solutions of the same problem:
are both
solutions of the same problem:
If you subtract these two problems from each other, and replace ![]() by
by ![]() , you get
, you get
The difference between two solutions of a linear problem always satisfies the homogeneous problem.
Now we must prove that ![]() is zero. That will mean that the
difference between
is zero. That will mean that the
difference between ![]() and
and ![]() is zero. And that will in turn
imply that
is zero. And that will in turn
imply that ![]() and
and ![]() must be the same; different solutions are
not possible.
must be the same; different solutions are
not possible.
To prove that ![]() is zero, the trick is to multiply the Laplace equation
for
is zero, the trick is to multiply the Laplace equation
for ![]() by
by ![]() and integrate over the entire domain
and integrate over the entire domain ![]() :
:
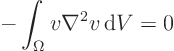
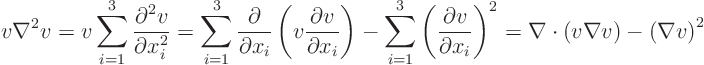
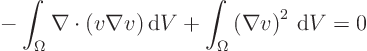
Now consider some special cases, starting with the simplest one:
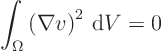
So ![]() must be zero everywhere, and that means that
must be zero everywhere, and that means that ![]() must
equal some constant
must
equal some constant ![]() everywhere. That includes that
everywhere. That includes that ![]() must be
must be
![]() on the boundary. But
on the boundary. But ![]()
![]() 0 on the boundary, so
0 on the boundary, so ![]() must be
zero. So
must be
zero. So ![]() is everywhere zero. So the difference between any two
solutions
is everywhere zero. So the difference between any two
solutions ![]() and
and ![]() of the original problem must be everywhere
zero. That means that the solutions must be equal, different
solutions are not possible. So the solution is unique.
of the original problem must be everywhere
zero. That means that the solutions must be equal, different
solutions are not possible. So the solution is unique.
So solutions of the Neumann problem are not unique. However, different solutions differ only by a constant, nothing more than that.
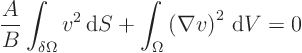 |
(18.5) |
To do that, note that in that case the final integral must again be zero. The final integral cannot be negative because it is an integral of a square. And the final integral cannot be positive; otherwise the first term in the sum above would have to be negative to make their sum zero. And the first term cannot be negative because it too is an integral of a square.
Since the second integral is zero, ![]() must again be some constant
must again be some constant
![]() . And since
. And since ![]() is nonzero at at least some point, (otherwise it
would be the pure Neumann problem), it follows from the boundary
condition that the constant is zero. So like the Dirichlet problem,
the solution is unique.
is nonzero at at least some point, (otherwise it
would be the pure Neumann problem), it follows from the boundary
condition that the constant is zero. So like the Dirichlet problem,
the solution is unique.
In that case, the first, surface, integral in (18.4) is a
sum over all these parts. As long as you can show that the combined
integral is zero or negative, ![]() must be zero and the solution is
unique. (Except that in the pure Neumann case, the solution
is indeterminate by a constant.)
must be zero and the solution is
unique. (Except that in the pure Neumann case, the solution
is indeterminate by a constant.)
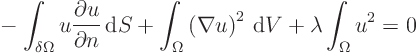 |
(18.6) |
Show that the Poisson equation
Using the arguments given in the text, uniqueness can not be shown for the Poisson equation
For the heat equation, similar arguments can be made as for the Laplace equation. This subsection briefly indicates the general lines.
Like for the Laplace equation in the previous subsection, the
difference ![]() between any two solutions of a heat equation
problem must satisfy the homogenous problem. That problem is here
between any two solutions of a heat equation
problem must satisfy the homogenous problem. That problem is here
Multiply the partial differential equation by ![]() and
integrate like for the Laplace equation to get
and
integrate like for the Laplace equation to get
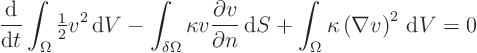 |
(18.7) |
Now consider conditions like those for the Laplace equation; Dirichlet
or Neumann boundary conditions, or mixed boundary boundary conditions
where ![]() and
and ![]() have the same sign. For those the final two terms
cannot by negative. So the first term cannot be positive. So the
have the same sign. For those the final two terms
cannot by negative. So the first term cannot be positive. So the
energy integral
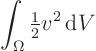
If the difference between two solutions is always zero, different solutions are not possible. Solutions are unique.
Under the same conditions on the boundary conditions, you can see that
one condition for properly posedness is satisfied: small changes in
the initial conditions produce small changes in the solution. To see
this, allow a nonzero initial condition for ![]() in the arguments
above. The energy integral for
in the arguments
above. The energy integral for ![]() at a later time is still never
larger than the energy integral of the initial condition for
at a later time is still never
larger than the energy integral of the initial condition for ![]() . And
the energy integral is a measure for the magnitude of
. And
the energy integral is a measure for the magnitude of ![]() : if you
divide the energy integral by half the volume of the domain and take a
square root, it gives the root mean square value of
: if you
divide the energy integral by half the volume of the domain and take a
square root, it gives the root mean square value of ![]() .
.
For the wave equation, similar arguments can be made as for the Laplace and heat equations. This subsection briefly indicates the general lines.
Like in the previous two subsections, the difference ![]() between any two solutions of a wave equation problem must satisfy the
homogenous problem. That problem is here
between any two solutions of a wave equation problem must satisfy the
homogenous problem. That problem is here
Multiply by ![]() and integrate over
and integrate over ![]() as before using
the divergence theorem to get
as before using
the divergence theorem to get
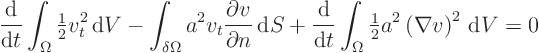 |
(18.8) |
Now consider conditions like those for the Laplace equation; Dirichlet
or Neumann boundary conditions, or mixed boundary boundary conditions
where ![]() and
and ![]() have the same sign. Under such conditions the surface
integral term cannot be negative. So the time derivative of the
have the same sign. Under such conditions the surface
integral term cannot be negative. So the time derivative of the
energy integral
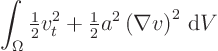
If the difference between two solutions is always zero, different solutions are not possible. Solutions are unique.
It may be noted that physically, the first term in the energy equation
is typically kinetic energy, and the second potential energy. If you
generalize the problem for ![]() to still have homogeneous boundary
conditions, but inhomogeneous initial conditions, you can derive
energy conservation. In particular for homogeneous Dirichlet or
Neumann boundary conditions, the total energy is preserved. For mixed
boundary conditions where
to still have homogeneous boundary
conditions, but inhomogeneous initial conditions, you can derive
energy conservation. In particular for homogeneous Dirichlet or
Neumann boundary conditions, the total energy is preserved. For mixed
boundary conditions where ![]() and
and ![]() have the same sign, the energy
can only decrease. If
have the same sign, the energy
can only decrease. If ![]() and
and ![]() have opposite sign, the problem is
unstable in the sense that the energy will increase. You can also use
this to show that small changes in the initial conditions produce
small changes in the solution for appropriate boundary conditions.
have opposite sign, the problem is
unstable in the sense that the energy will increase. You can also use
this to show that small changes in the initial conditions produce
small changes in the solution for appropriate boundary conditions.