24.3 A hyperbolic example

This example illustrates Laplace transform solution for a hyperbolic partial differential equation.

It also illustrates that the transformed coordinate is not always a time.

24.3.1 The physical problem

Find the horizontal perturbation velocity in a supersonic flow above a membrane overlaying a compressible variable medium.

**Figure 24.3:** Supersonic flow over a membrane.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex1.eps} \end{center} \end{figure}$

24.3.2 The mathematical problem

**Figure 24.4:** Supersonic flow over a membrane.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex2.eps} \end{center} \end{figure}$

Domain $\bar \Omega$ : 0 $\raisebox{-.3pt}{$\leqslant$}$ $\raisebox{.3pt}{$<$}$ $\infty, 0$ $\raisebox{-.3pt}{$\leqslant$}$ $\raisebox{.3pt}{$<$}$ $\infty$
Unknown horizontal perturbation velocity $\vphantom0\raisebox{1.5pt}{$=$}$
Hyperbolic
Two homogeneous initial conditions
One mixed boundary condition at $\vphantom0\raisebox{1.5pt}{$=$}$ 0 and a regularity constraint at $\vphantom0\raisebox{1.5pt}{$=$}$ $\infty$
Constant $\vphantom0\raisebox{1.5pt}{$=$}$ $\tan \mu$ , where $\mu$ is the Mach angle.

Try a Laplace transform. The physics and the fact that Laplace transforms like only initial conditions suggest that is the one to be transformed. Variable is our ``time-like'' coordinate.

24.3.3 Transform the problem

Transform the partial differential equation:

$\begin{displaymath} u_{xx} = a^2 u_{yy} \quad \stackrel{\hbox{Table 6.3, \ch... ...- \overline{\smash{u_x(0,y)}\vphantom{.}} = a^2 \hat u_{yy} \end{displaymath}$

Transform the boundary condition:

$\begin{displaymath} u_y - p u = f(x) \quad \Relbar\joinrel\Relbar\joinrel\... ...nrel\Longrightarrow \quad \hat u_y - p \hat u = \hat f(s) \end{displaymath}$

24.3.4 Solve the transformed problem

Solve the partial differential equation, again effectively a constant coefficient ordinary differential equation:

$\begin{displaymath} s^2 \hat u = a^2 \hat u_{yy} \end{displaymath}$

$\begin{displaymath} s^2 = a^2 k^2 \quad\quad\Rightarrow\quad\quad k = \pm s/a \end{displaymath}$

$\begin{displaymath} \hat u = A e^{sy/a} + B e^{-sy/a} \end{displaymath}$

Apply the boundary condition at $\vphantom0\raisebox{1.5pt}{$=$}$ $\infty$ :

$\begin{displaymath} A = 0 \end{displaymath}$

Apply the boundary condition at $\vphantom0\raisebox{1.5pt}{$=$}$ 0:

$\begin{displaymath} \hat u_y - p \hat u = \hat f \quad\quad\Rightarrow\quad\quad - \frac sa B - p B = \hat f \end{displaymath}$

Solving for and plugging it into the expression for $\hat u$ gives:

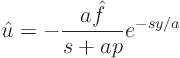
$\begin{displaymath} \hat u = - \frac{a\hat f}{s+ap} e^{-sy/a} \end{displaymath}$

24.3.5 Transform back

We need to find the original to

$\begin{displaymath} \hat u = - \frac{a}{s+ap} \hat f e^{-sy/a} \end{displaymath}$

Looking in the tables:

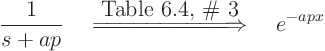
$\begin{displaymath} \frac{1}{s+ap} \quad \stackrel{\hbox{Table 6.4, \char93 ... ...\joinrel \Relbar\joinrel\Longrightarrow} \quad e^{-apx} \end{displaymath}$

The other factor is a shifted function , restricted to the interval that its argument is positive:

$\begin{displaymath} e^{-sy/a} \hat f \quad \stackrel{\hbox{Table 6.3, \char9... ...\Longrightarrow} \quad \bar f\left(x - \frac{y}{a}\right) \end{displaymath}$

With the bar, I indicate that I only want the part of the function for which the argument is positive. This could be written instead as

$\begin{displaymath} f\left(x - \frac{y}{a}\right) H \left(x - \frac{y}{a}\right) \end{displaymath}$

where the Heaviside step function

$\vphantom0\raisebox{1.5pt}{$=$}$ 0 if

is negative and 1 if it is positive.

**Figure 24.5:** Function $\bar f$ .
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex3.eps} \end{center} \end{figure}$

Use convolution, Table 6.3, # 7. again to get the product.

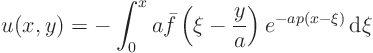
$\begin{displaymath} u(x,y) = - \int_0^x a \bar f\left(\xi - \frac{y}{a}\right) e^{-ap(x-\xi)} { \rm d}\xi \end{displaymath}$

This must be cleaned up. I do not want bars or step functions in my answer.

I can do that by restricting the range of integration to only those values for which $\bar f$ is nonzero. (Or is nonzero, if you prefer)

**Figure 24.6:** Function $\bar f$ again.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex3.eps} \end{center} \end{figure}$

Two cases now exist:

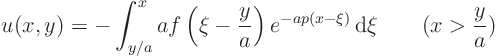
$\begin{displaymath} u(x,y) = - \int_{y/a}^x a f\left(\xi - \frac{y}{a}\right) e^{-ap(x-\xi)} { \rm d}\xi \qquad (x > \frac ya) \end{displaymath}$

$\begin{displaymath} u(x,y) = 0 \qquad (x < \frac ya) \end{displaymath}$

It is neater if the integration variable is the argument of . So, define $\phi$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\xi - y/a$ and convert:

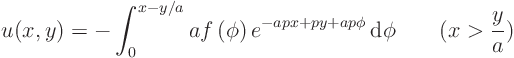
$\begin{displaymath} u(x,y) = - \int_{0}^{x-y/a} a f\left(\phi\right) e^{-apx+py+ap\phi} { \rm d}\phi \qquad (x > \frac ya) \end{displaymath}$

$\begin{displaymath} u(x,y) = 0 \qquad (x < \frac ya) \end{displaymath}$

This allows me to see which physical

values I actually integrate over when finding the flow at an arbitrary point:

**Figure 24.7:** Supersonic flow over a membrane.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex4.eps} \end{center} \end{figure}$

24.3.6 An alternate procedure

An alternate solution procedure is to define a new unknown:

$\begin{displaymath} v \equiv u_y - p u \end{displaymath}$

You must derive the problem for v:

The boundary condition is simply:

$\begin{displaymath} v(x,0) = f(x) \end{displaymath}$

To get the partial differential equation for , use

$\begin{displaymath} \frac{\partial [P.D.E.]}{\partial y} - p [P.D.E.] \quad\quad\Rightarrow\quad\quad v_{tt} = a^2 v_{xx} \end{displaymath}$

Similarly, for the initial conditions:

$\begin{displaymath} \frac{\partial [I.C.]}{\partial y} - p [I.C.] \quad\quad\Rightarrow\quad\quad v(0,y) = v_x(0,y) = 0 \end{displaymath}$

**Figure 24.8:** Problem for v.
$\begin{figure} \begin{center} \leavevmode {} \epsffile{laphex5.eps} \end{center} \end{figure}$

After finding , I still need to find from the definition of :

$\begin{displaymath} v \equiv u_y - p u \end{displaymath}$

Where do you get the integration constant??