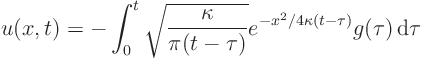|
|
|
|
|
Next: 24.3 A hyperbolic example |
|
This example illustrates Laplace transform solution for a parabolic partial differential equation.
Find the flow velocity in a viscous fluid being dragged along by an accelerating plate.
Try a Laplace transform in ![]() .
.
Transform the partial differential equation:
Transform the boundary condition:
Solve the partial differential equation:
Apply the boundary condition at ![]()
![]()
![]() that
that ![]() must be
regular there:
must be
regular there:
Apply the given boundary condition at ![]()
![]() 0:
0:
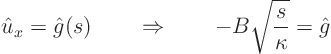
Solving for ![]() and plugging it into the solution of the ordinary
differential equation,
and plugging it into the solution of the ordinary
differential equation, ![]() has been found:
has been found:
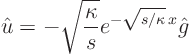
We need to find the original function ![]() corresponding to the transformed
corresponding to the transformed
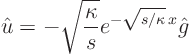
We do not really know what ![]() is, just that it transforms back
to
is, just that it transforms back
to ![]() . However, we can find the other part of
. However, we can find the other part of ![]() in the
tables.
in the
tables.
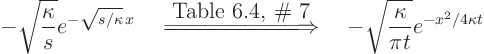
How does ![]() times this function transform back? The product of
two functions, say
times this function transform back? The product of
two functions, say ![]() , does not transform back
to
, does not transform back
to ![]() . The convolution theorem Table 6.3 # 7 is needed:
. The convolution theorem Table 6.3 # 7 is needed: