|
|
|
|
|
Next: 2.3 General Approach |
|
From [1, p. 116, 30]
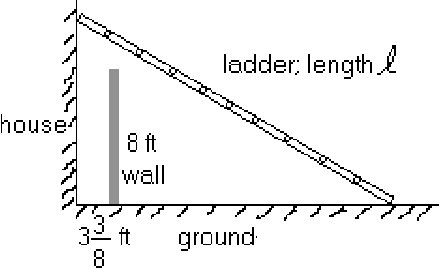
Given: A free standing wall, located ![]() ft from
the side of a house.
ft from
the side of a house.
Asked: What is the length ![]() of the shortest ladder that can
reach the house (over the free standing wall).
of the shortest ladder that can
reach the house (over the free standing wall).
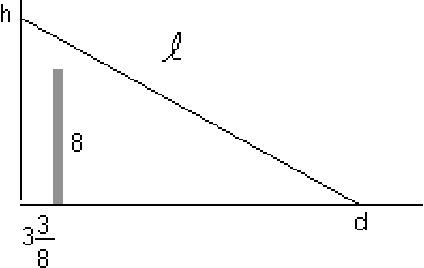
Two degrees of freedom: say ![]() and
and ![]()
One inequality constraint: the ladder must be above the free standing wall.
The shortest ladder hits the free standing wall:
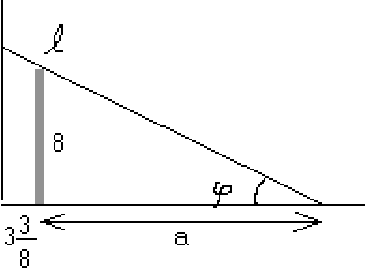
One degree of freedom left: ![]() .
.
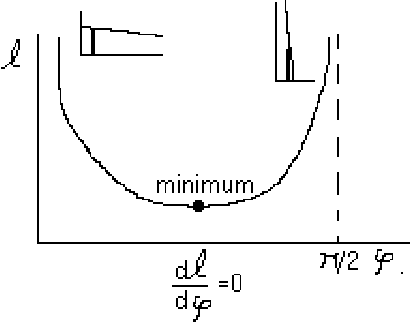
At the minimum:
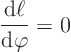

First find ![]() :
:
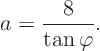
Then:
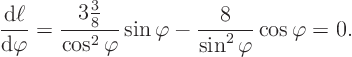
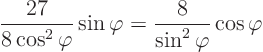
From (2.1)