|
|
|
|
|
Next: 3. Approximations |
|
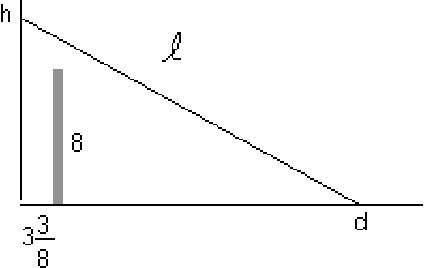
If you do not know a priori that the ladder hits the wall, you can follow the general approach.
There are now two degrees of freedom. They are conveniently taken to
be ![]() and
and ![]() .
.
Then the length of the ladder is, (from Pythagoras),
We now need to figure out what values of ![]() and
and ![]() produce the
shortest ladder.
produce the
shortest ladder.

Note that by the definition of the problem, ![]()
![]() 8 and
8 and ![]()
![]()
![]() . But these constraints are not precise. For example,
. But these constraints are not precise. For example, ![]()
![]() 8.001 and
8.001 and ![]()
![]()
![]() would obviously have the
ladder go through the wall.
would obviously have the
ladder go through the wall.
There is a precise constraint, that the ladder cannot pass through the
wall. If ![]() is the height of the point on the ladder straight above
the wall, then similar triangles give:
is the height of the point on the ladder straight above
the wall, then similar triangles give:
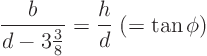
![\begin{displaymath}
h \frac{d - {\textstyle 3\frac38}}{d} \ge 8
\quad\quad\Rightarrow\quad\quad h [d - 3\frac38] - 8d \ge 0
\end{displaymath}](img96.gif)
So the problem is to minimize
To solve this, first plot the possible ![]() and
and ![]() values:
values:
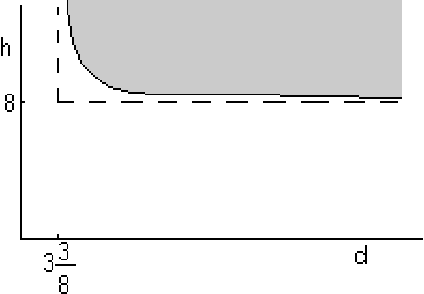
Now you must figure out whether the shortest ladder occurs in the strict interior of the grey region or on its boundary. Try the interior first.

For a minimum, at least locally, in the strict interior of the
grey region, the partial derivatives must be zero.

Since the minimum is not in the interior, it must be on the boundary
of the grey region. Now obviously for infinite ![]() or
or ![]() or both you
do not have the shortest ladder. So the minimum cannot be on the
boundary at infinity. It must be on the curve where the ladder just
hits the wall.
or both you
do not have the shortest ladder. So the minimum cannot be on the
boundary at infinity. It must be on the curve where the ladder just
hits the wall.
But how do we find the minimum on this line? The partial derivatives
of ![]() are not zero at this point. (Just check that out in the
previous subsection.)
are not zero at this point. (Just check that out in the
previous subsection.)
The trick is to define an artificial third variable ![]() , called
a
, called
a Lagrangian multiplier,
corresponding to the
constraint. (In the most general case, this Lagrangian multiplier has
no particular physical meaning.) Then define a new function ![]() to
replace
to
replace ![]() in the minimization:
in the minimization:
Now it turns out that you can find the desired minimum by finding an
unconstrained stationary point to this function ![]() :
:
![\begin{eqnarray*}
& \partial f/\partial d = (h^2 + d^2)^{-1/2}d + \lambda (h -...
...ial f/\partial \lambda = h [d - {\textstyle 3\frac38}] - 8d = 0
\end{eqnarray*}](img103.gif)
From the first two equations
If you would have more than one constraint, there is one separate Lagrangian multiplier for each one. For example, if you take care of the boundary conditions in a finite element computation this way, you will get one for each boundary condition at each boundary point.