|
|
|
|
|
Next: 19.3 The Poisson or Laplace equation in a finite region |
|
(Book, section 8.2)
This section works out the Green’s function idea for the Poisson
equation
In this section, the Green’s function in infinite two-dimensional space will be derived. For discussion purposes, the problem will be assumed to be heat conduction in a plate, but the mathematical solution does not depend on what the physical meaning is. In the homework you will derive the Green’s function for the Poisson equation in infinite three-dimensional space; the analysis is similar but the result will be quite different.
First of all, a Green’s function ![]() for the above problem is by
definition a solution when function
for the above problem is by
definition a solution when function ![]() is a delta function. A delta
function is an infinitely narrow spike that integrates to one. We
will write
is a delta function. A delta
function is an infinitely narrow spike that integrates to one. We
will write ![]() for the point at which the temperature is
desired. Further
for the point at which the temperature is
desired. Further ![]() is the position of the delta function.
is the position of the delta function.
In two dimensions ![]()
![]()
![]() and
and ![]()
![]()
![]() . Also, the two-dimensional delta function can be written in
terms of one-dimensional ones as
. Also, the two-dimensional delta function can be written in
terms of one-dimensional ones as
In any number of dimensions, the Green’s function solution of the
Poisson equation with a delta function as right hand side will be
written as
In terms of the Green’s function, the solution ![]() to the Poisson
equation with an arbitrary right hand side
to the Poisson
equation with an arbitrary right hand side ![]() can be written as
can be written as
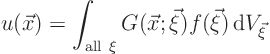 |
(19.3) |
volumeintegral over all components of vector
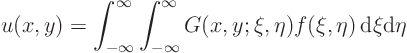 |
(19.4) |
volumeis here really an area.
It will be found that the Green’s function for the two-dimensional
infinite-domain Poisson problem is:
Similarly, you will find in the homework that the Green’s function for
the three-dimensional infinite-domain Poisson problem is:
Therefore the two-dimensional temperature distribution ![]() corresponding to a general distribution of added heat
corresponding to a general distribution of added heat
![]() is:
is:
Given an added-heat distribution ![]() , you can find the temperature
distribution
, you can find the temperature
distribution ![]() by doing the corresponding integral. Especially if
you only want the temperature at a few points, this can be quite
effective. (If you want the temperature at essentially all points, a
by doing the corresponding integral. Especially if
you only want the temperature at a few points, this can be quite
effective. (If you want the temperature at essentially all points, a
multigrid
numerical method that directly solves the
partial differential equation is far more efficient. However, there
are so-called fast-summation
methods, like the one by
Van Dommelen and Ründensteiner, that can do the integrals very fast
too, especially if the region of heat addition is limited.)
The physical meaning of the Green’s function varies with setting. In heat transfer, it is the solution for a point heat source, in electrostatics a point charge, in gravitation a point mass, in potential flows a point source of fluid, in two-dimensional vortex flows a point vortex, etcetera.
To verify the two-dimensional Green’s function ![]() given in the
previous section, the solution to the Poisson equation must be found
in which
given in the
previous section, the solution to the Poisson equation must be found
in which ![]() is a delta function spike at some point
is a delta function spike at some point ![]() .
.
However, dealing with infinite functions like delta functions is a
very abstract and fishy problem. Therefore an approach like in the
first section will be used. It will assumed that we are really trying
to solve the Poisson equation for an arbitrary function ![]() . (And so
we are, really.) We then mentally cut up this function
. (And so
we are, really.) We then mentally cut up this function ![]() into
spikes. That idea is sketched in two-dimensions in figure
fig:2dspike.
into
spikes. That idea is sketched in two-dimensions in figure
fig:2dspike.
![\begin{figure}
\begin{center}
\leavevmode
{}
\setlength{\unitlength}{1p...
...\makebox(0,0)[l]{$f(\xi,\eta)$}}
\end{picture}
\end{center}
\end{figure}](img1086.gif) |
The problem for such a narrow, but finite spike can be solved with
some physical intuition. The solution will again be called
![]() . The total solution will then be the sum of the solutions
. The total solution will then be the sum of the solutions
![]() for all the spikes. Of course, each solution will not
just depend on the position
for all the spikes. Of course, each solution will not
just depend on the position ![]() at which you want to know the
temperature. It will also depends on where the spike is, as indicated
by its center point
at which you want to know the
temperature. It will also depends on where the spike is, as indicated
by its center point ![]() .
.
![\begin{figure}
\begin{center}
\leavevmode
{}
\setlength{\unitlength}{1p...
...-19,40){\makebox(0,0)[l]{$r=d$}}
\end{picture}
\end{center}
\end{figure}](img1087.gif) |
Figure 19.7 shows a two-dimensional top view equivalent to
figure 19.6. In other words, it shows just the plate,
not the function ![]() . The dimensions of the little rectangle to which
the heat is added by the considered spike will be indicated by
. The dimensions of the little rectangle to which
the heat is added by the considered spike will be indicated by
![]() . The amount of heat added is
. The amount of heat added is
![]() , since variations in
, since variations in ![]() over the
small rectangle can be ignored. Since the Green’s function
over the
small rectangle can be ignored. Since the Green’s function ![]() is
the solution for unit added heat flux, the final Green’s
function will be obtained by dividing the solution
is
the solution for unit added heat flux, the final Green’s
function will be obtained by dividing the solution ![]() by the
amount of heat
by the
amount of heat ![]() . (Formally speaking,
you would then still need to take the limit
. (Formally speaking,
you would then still need to take the limit ![]() , but that becomes trivial under the approximations to be made.)
, but that becomes trivial under the approximations to be made.)
The mathematical problem being solved is:
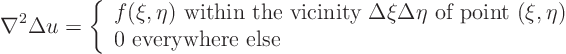
For convenience, for now use a polar coordinate system ![]() centered around the point
centered around the point ![]() of heat addition, as indicated
in figure 19.7. Further, since the rectangle
of heat addition, as indicated
in figure 19.7. Further, since the rectangle
![]() is assumed to be very small, almost a single
point, you can reasonably assume that the temperature distribution
is assumed to be very small, almost a single
point, you can reasonably assume that the temperature distribution
![]() depends only on the distance
depends only on the distance ![]() from the point where the
heat is added, not on
from the point where the
heat is added, not on ![]() .
.
Under those assumptions, it is easiest to simply integrate the
mathematical problem above over the inside of a circle of radius ![]() :
:
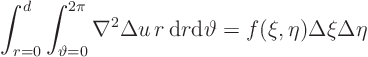
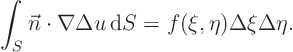
In this two-dimensional problem the surface
![]() is the
perimeter
is the
perimeter ![]() of the circle. And
of the circle. And ![]() is the radial polar
unit vector
is the radial polar
unit vector ![]() , which makes the total derivative
, which makes the total derivative
![]() equal to the derivative with respect
to radius,
equal to the derivative with respect
to radius, ![]() . So you have:
. So you have:
Do an analysis similar to either this subsection, or the next one, to derive the Green’s function of the Poisson equation in three dimensional infinite space.
For students who do not like the above derivation with infinitesimal regions, and the assumption that their temperature distribution only depends on distance, here is a mathematically solid derivation.
It will be assumed that a suitable heat distribution ![]() is given
with at least continuous low-order derivatives. Also that it
disappears sufficiently quickly at large distances that you do not have
to worry about that region. Then it is to be shown that if you do the
Green’s function integration
is given
with at least continuous low-order derivatives. Also that it
disappears sufficiently quickly at large distances that you do not have
to worry about that region. Then it is to be shown that if you do the
Green’s function integration
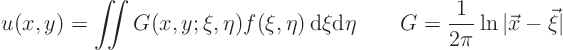
![\begin{figure}
\begin{center}
\leavevmode
{}
\setlength{\unitlength}{1p...
...150){\makebox(0,0)[l]{$\rho=R$}}
\end{picture}
\end{center}
\end{figure}](img1110.gif) |
The first thing to check is that you do at least get some
function ![]() by doing the integration. That is not automatic,
since the integrand is infinite when
by doing the integration. That is not automatic,
since the integrand is infinite when ![]()
![]()
![]() . And
integration over an infinite region is not proper either. What you
must do is exclude the inside of a very small circle around
. And
integration over an infinite region is not proper either. What you
must do is exclude the inside of a very small circle around ![]() and the outside of a very large circle from the integration. Then you
define
and the outside of a very large circle from the integration. Then you
define ![]() to be the limit of the integral when the radius of the
small circle
to be the limit of the integral when the radius of the
small circle ![]() becomes zero, and the radius
becomes zero, and the radius ![]() of the the
large circle becomes infinite. (Assuming that those limits exist.)
See figure 19.8.
of the the
large circle becomes infinite. (Assuming that those limits exist.)
See figure 19.8.
A local polar coordinate system ![]() will be used centered at
the point
will be used centered at
the point ![]() at which the temperature is desired. Then
at which the temperature is desired. Then ![]() is
the distance that the heat addition point
is
the distance that the heat addition point ![]() is away from
the point
is away from
the point ![]() at which the temperature is desired. Note that the
variables in the integration are
at which the temperature is desired. Note that the
variables in the integration are ![]() and
and ![]() ;
; ![]() is just a
fixed point in this entire story. The two-dimensional Green’s
function is
is just a
fixed point in this entire story. The two-dimensional Green’s
function is
The effect of the excluded area outside the large circle may be taken
to be vanishingly small if the radius of the large circle, call it
![]() , is large, since it was assumed that function
, is large, since it was assumed that function ![]() vanishes
sufficiently quickly at large distances. The effect of the excluded
area inside the small circle is can be estimated as
vanishes
sufficiently quickly at large distances. The effect of the excluded
area inside the small circle is can be estimated as
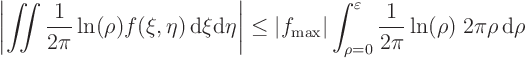
But does it satisfy the Poisson equation ![]()
![]()
![]() ? Now what you
cannot do here is simply differentiate the Green’s function
(the logarithm) within the integral
? Now what you
cannot do here is simply differentiate the Green’s function
(the logarithm) within the integral
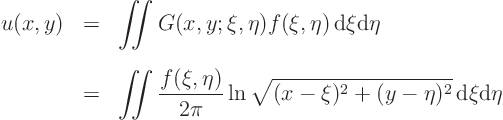
Instead you need to go back to the basic definition of the partial
derivatives. As an example, take
The integral for ![]() ;
;
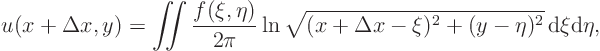
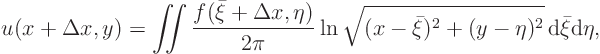
Plug this, and the expression for ![]() itself, into the limit
above to get:
itself, into the limit
above to get:
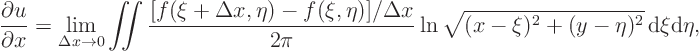
The net result is that
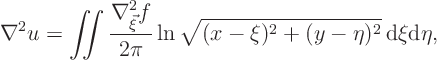
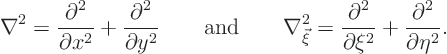
Now you need to show that the integral in the right hand side is equal
to ![]() to finish the proof that
to finish the proof that ![]()
![]()
![]() . To shorten the
notations, the Green’s function will again be written as
. To shorten the
notations, the Green’s function will again be written as ![]() , and
the question is whether
, and
the question is whether
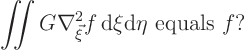
If you add a second term,
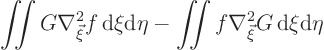
Green’s second identity now says that the expression that should equal
![]() is the
is the surface
integral
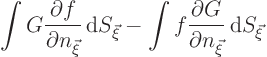
surface
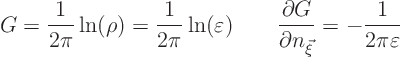
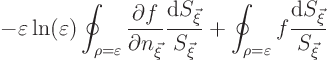
So finally, you conclude that ![]() is indeed
is indeed ![]() .
.