19.1 Introduction

The purpose of this section is to introduce the Green’s function ideas.

19.1.1 The one-dimensional Poisson equation

This subsection will consider a very simple problem, the Poisson equation in one-di­men­sion­al infinite space. The solution will be obtained using a Green’s function approach.

In general, the Poisson equation reads

$$\nabla^2 u = f$$

where $f$ is a given function and $u$ the unknown to be found. In one-di­men­sion­al infinite space that becomes

$$u_{xx} = f(x) \qquad -\infty < x \infty$$

Of course, this equation is trivial to solve. That makes it such a good example to understand the Green’s function approach.

It may be noted that the solution is not quite unique; adding $A+Bx$ to any solution, with $A$ and $B$ constants, produces another solution. Therefore, solving the problem will simply be taken to be finding a solution, whichever one.

Figure 19.1: Chopping a one-dimensional function up into spikes.

Figure 19.1 shows a sketch of an arbitrary given function $f(x)$.

The basic idea of a Green’s function approach is to chop the function into narrow spikes and solve for each spike separately.

Figure 19.2: Contribution of one spike to the solution.

Consider an arbitrary example spike, shown in grey in figure 19.1. Figure 19.2 shows this one spike separately. The solution due to this one spike, call it ${\Delta}u$, is shown in red. The total solution can be obtained by summing the solutions for all the spikes together:

$$u = \sum_{{\rm all spikes}} \Delta u$$

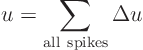
To be sure, solving the problems for the spikes exactly is just as difficult as solving the original problem. But if the spikes are narrow, approximations can be made. Before doing so however, consider the exact solution ${\Delta}u$ in figure 19.2 more closely. Note that the solution is linear everywhere except in the narrow region of the spike. That is because it satisfies the Poisson equation

$$\Delta u_{xx} = \Delta f$$

Here ${\Delta}f$ is the single-spike function, shown in green in figure 19.2. It is zero everywhere outside the single spike, because the other spikes are emitted. So outside the single spike, the second derivative of ${\Delta}u$ is zero. And if its second derivative is zero, then ${\Delta}u$ is linear.

The slope does change from one side of the spike region to the other. In fact, integration of the equation above produces

$$\Delta u_{x,\rm after} - \Delta u_{x,\rm before} = \int_{\rm spike} f(\xi'){ \rm d}\xi'$$

Note that the integral is the spike area. So the slope changes by an amount equal to the spike area. Since the spike area is small for small $\Delta\xi$, so is change in slope. Figure 19.2 shows a sketch how the solution $\Delta{u}$ looks. It took the slopes equal and opposite at both sides. That keeps the maximum slope as small as possible.

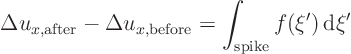
If we approximate the spike area as $f(\xi) \Delta\xi$, where $\xi$ is the center point of the spike, we get

$$\Delta u_{x,\rm after} - \Delta u_{x,\rm before} \approx f(\xi) \Delta\xi$$

Now first consider an idealized spike problem. In this idealized spike problem, the spike is given a unit area. Then the limit is taken that the width of the spike becomes zero. (In that limit, the height of the spike must go to infinity to keep the area constant.) The limiting infinitely narrow, infinitely high, spike is called the “Dirac delta function” $\delta(x-\xi)$.

The corresponding solution $\Delta{u}$ is called the Green’s function $G(x;\xi)$. It is equal to

$$\fbox{$\displaystyle G(x;\xi) = {\textstyle\frac{1}{2}} \vert x-\xi\vert $} %$$ (19.1)

That is easily checked. Indeed, it is linear at both sides of point $\xi$. And for $x$ $\raisebox{.3pt}{$>$}$ $\xi$, the absolute signs do nothing, so the slope is ${\textstyle\frac{1}{2}}$. For $x$ $\raisebox{.3pt}{$<$}$ $\xi$, the absolute signs produce a minus sign so the slope is $-{\textstyle\frac{1}{2}}$. That makes the total change in slope 1, the area of the delta function, as it should.

Figure 19.3: Approximation of the spike by an infinitely narrow one.

Back to the original spike of small area $f(\xi) \Delta\xi$. We can approximate its solution in terms of the Green’s function above as

$$\Delta u \approx G(x;\xi)f(\xi) \Delta\xi$$

Since the Green’s function has a unit change in slope, multiplying by the spike area gives the correct change in slope. The idea is shown in figure 19.3. We replace the narrow spike by an infinitely narrow one, but still with the same area. That gives essentially the same solution as in figure 19.2. (There will be small deviations. In particular, the solution for the infinite thin spike will be linear right up to the point $\xi$ while the original was somewhat rounded. But these differences can be neglected.)

The total solution $u$ to the original problem is obtained by summing the contribution of all the spikes:

$$u = \sum_{{\rm all spikes}} \Delta u \approx \sum_{{\rm all spikes}} G(x,\xi) f(\xi) \Delta\xi$$

To make this exact, we take the limit that the width $\Delta\xi$ of the spikes becomes zero. In that limit, the summation becomes integration. The exact solution of the Poisson equation is therefore:

$$\fbox{$\displaystyle u_{xx} = f(x) \quad -\infty < x < \... ... \int_{\xi=-\infty}^\infty G(x;\xi) f(\xi){ \rm d}\xi $} %$$ (19.2)

where $G(x;\xi)$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\textstyle\frac{1}{2}}\vert x-\xi\vert$. You can verify this solution by splitting the integral into two and integrating by parts. It is somewhat messy to do so, however.

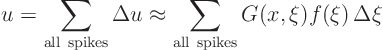
Example

Question: Find Green’s function approximations to the solution $u$ of the Poisson problem

$$u_{xx} = -2 x e^{-x^2} \qquad -\infty < x < \infty$$

Use various spike widths $\Delta\xi$. Verify that you do seem to get the exact solution when $\Delta\xi\to0$ as claimed above.

Solution:

Figure 19.4 shows some results obtained using matlab. First of all, this problem has an exact solution

$$\frac{\sqrt{\pi}}{2} {\rm erf}(x)$$

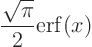
where erf is the so-called error function. This exact solution is indicated by the blue dots in figure 19.4.

Figure 19.4: Green’s function solution of an example one-dimensional Poisson equation.

The question is now, how good is a Green’s function approximation for this problem?

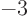
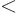
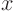
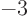
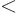
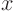
The right hand side in the Poisson problem is negligibly small outside the range $-3$ $\raisebox{.3pt}{$<$}$ $x$ $\raisebox{.3pt}{$<$}$ 3, so no spikes are needed outside that range. In the top left graph, the interval $-3$ $\raisebox{.3pt}{$<$}$ $x$ $\raisebox{.3pt}{$<$}$ 3 was chopped up into two spikes. Each spike was approximated by a delta function spike at its center as described above. Then the two Green’s function solutions of these spikes were added to give the red solid line. You can see the locations of the delta functions from the kinks in this solution. Obviously, this Green’s function solution is not accurate.

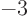
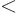
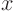
It gets better if the interval $-3$ $\raisebox{.3pt}{$<$}$ $x$ $\raisebox{.3pt}{$<$}$ 3 is divided up into 5 narrower spikes, and each one is approximated by a delta function spike. The solution for that is shown in the top right graph of figure 19.4. The next graph shows that for 10 spikes, the Green’s function solution is quite close to the exact solution. However, there are still visible kinks at the locations of the delta function spikes. At 20 spikes, the kinks are virtually invisible.

19.1.1 Review Questions

1.

Solve the Poisson equation

$$u_{xx} = - 2 \frac{\sinh x}{\cosh^3 x}$$

numerically using Green’s functions. Experiment with numerical parameters and show convergence.

Include your code.

Solution gf1d-a

2.

Show that

$$\tilde u(x) = \int_{\xi =-\infty}^\infty{\textstyle\frac{1}{2}}\vert x-\xi\vert f(\xi){ \rm d}\xi$$

is a solution to

$$u_{xx} = f(x) \quad -\infty < x < \infty$$

You can assume that function $f(\xi)$ becomes zero rapidly at large $\xi$. (If you want, you can assume it is zero beyond some value $\xi_{\rm {max}}$ of $\vert\xi\vert$.) Find out what function $\tilde{u}$ is relative to some given second anti-derivative $u_0$ of $f$.

Solution gf1d-b

19.1.2 More on delta and Green’s functions

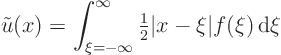
Figure 19.5 shows the definition of the one-di­men­sion­al delta function. Note that the function value of $\delta(x-\xi)$ is zero at all points except at the single point $\xi$. At that single point however, the function value is infinite.

Figure 19.5: Approximate Dirac delta function $\delta_\varepsilon(x-\xi)$ is shown left. The true delta function $\delta(x-\xi)$ is the limit when $\varepsilon$ becomes zero, and is an infinitely high, infinitely thin spike, whose bottom is shown right.

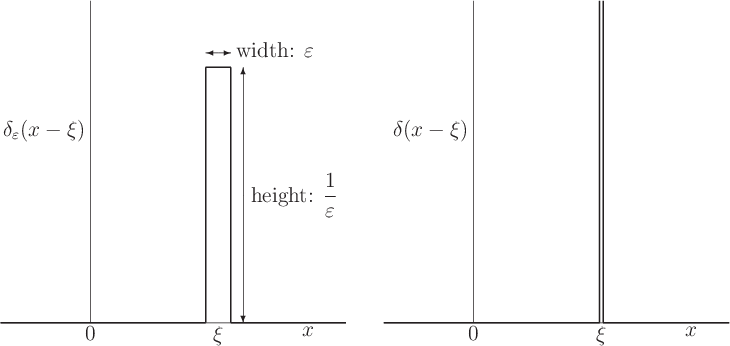Of course, infinite function values are invalid mathematics. The delta function is not a properly defined function. The best way to deal with that as an engineer is to mentally not make the delta function infinitely narrow. Instead think of a delta function as an extremely narrow, extremely high spike that integrates to 1. Mathematicians have better but more complicated ways of dealing with the problem, {A.1}.

Usually delta functions are used as inhomogeneous terms in differential equation problems. The solutions to these problems are called Green’s functions. Fortunately, it turns out that while the delta function is not well defined, the Green’s function typically is. In the limit that the width of the delta function becomes zero, the Green’s function stays a perfectly good function.

For example, the Green's function of the Poisson equation in one dimension formally satisfies

$$\frac{\partial^2 G(x;\xi)}{\partial x^2} = \delta(x-\xi) \quad -\infty < x < \infty$$

You can make this equation meaningful by replacing the delta function by the approximate delta function of figure 19.5 and then taking the limit that the width $\varepsilon$ becomes zero. In that limit, the right hand side becomes the poorly defined delta function. However, as discussed in the previous section, $G(x;\xi)$ becomes ${\textstyle\frac{1}{2}}\vert x-\xi\vert$. That is a mathematically completely legal function.

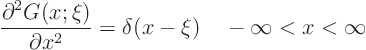
Another thing to note is that Green’s functions in infinite domains are usually not unique. The most general Green’s function for the Poisson equation in one dimension is

$$G(x;\xi) = {\textstyle\frac{1}{2}} \vert x-\xi\vert + A + B x$$

where $A$ and $B$ are arbitrary constants. The final two terms are a solution of the homogeneous equation.

You would typically like the Green’s function to be zero at large distances. But for the one dimensional Green’s function above, (as well as for the two-di­men­sion­al equivalent, for that matter), there is no way to do it. There is no way to choose $A$ and $B$ so that $G$ is zero at both $\pm\infty$. The best you can do is make the derivatives at $\pm\infty$ as small as possible. If $B$ is nonzero, the derivative at either $-\infty$ or $\infty$ is greater than $\frac12$ in magnitude. So you take $B$ zero so that neither derivative exceeds $\frac12$ in magnitude. There is nothing defensible that you can take for the constant $A$, so you take it also zero.

It may be noted that in wave propagation problems, trying to make the wave function as small as possible typically does not work. Instead you take the Green’s function so that at large distances it describes waves that move away to infinity. Green’s functions that describe waves that come in from infinity are physically undesirable.