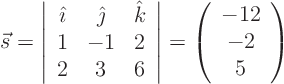10.2 Example

From [1, p. 439, 35(b)].

Asked: The line through point 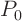$P_0$, (2,-3,5), and parallel to the line $x-y+2z+4=0$, $2x+3y+6z-12=0$.

$$\epsffile{vecgeom1.eps}$$

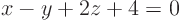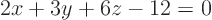10.2.1 Identification

$$\epsffile{vecgeom1.eps}$$

• I need a vector in the direction of the desired line.
• This is the same direction as the given line.
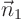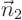• The two equations give me vectors $\vec n_1$ and $\vec n_2$ normal to the given line
• Cross the two vectors!

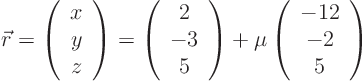
10.2.2 Solution

$$x-y+2z+4=0 \quad\quad\Rightarrow\quad\quad \vec n_1 = (1,-1,2)$$

$$2x+3y+6z-12=0 \quad\quad\Rightarrow\quad\quad \vec n_2 = (2,3,6)$$

$$\vec s = \left\vert \begin{array}{ccc} {\hat\imath}& {... ... = \left( \begin{array}{c} -12 -2 5 \end{array} \right)$$

$$\vec r = \left(\begin{array}{c} x y z \end{array} \r... ...mu \left( \begin{array}{c} -12 -2 5 \end{array} \right)$$

Alternatively:

$$\frac{x-2}{-12} = \frac{y+3}{-2} = \frac{z-5}{5} (= \mu)$$