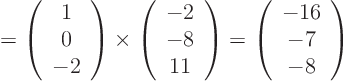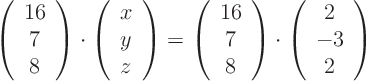| Analysis in Mechanical Engineering |
|
© Leon van Dommelen |
|
Subsections
10.3 Example
From [1, p. 440, 36(b)].
Asked:
The plane through point 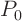 , (2,-3,2), and the line
, (2,-3,2), and the line
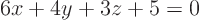 ,
, 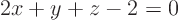 .
.
10.3.1 Identification
- I need a vector normal to the plane.
- I can get this by crossing two vectors in the plane.
- One such vector is
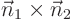 .
.
- To find another, find any point
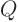 on the line,
then
on the line,
then 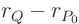 is in the plane.
is in the plane.
10.3.2 Solution
When 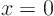 on the line,
on the line,
![]() , (2,-3,2), and the line
, (2,-3,2), and the line
![]() ,
, ![]() .
.


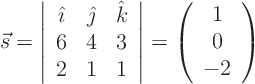
![]() on the line,
on the line,
![\begin{displaymath}
\vec n = \left(\begin{array}{c} 1 0 -2 \end{array} \...
...ft( \begin{array}{c} 2 -3 2 \end{array} \right) \right]
\end{displaymath}](img348.gif)