| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.27 Details of the animations
This note explains how the wave packet animations of chapter
7.11 and 7.12 were obtained. If you want a
better understanding of unsteady solutions of the Schrödinger
equation and their boundary conditions, this is a good place to start.
In fact, deriving such solutions is a popular item in quantum
mechanics books for physicists.
First consider the wave packet of the particle in free space, as shown
in chapter 7.11.1. An energy eigenfunction with energy
 in free space takes the general form
in free space takes the general form
where 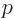 is the momentum of the particle and
is the momentum of the particle and 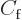 and
and
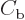 are constants.
are constants.
To study a single wave packet coming in from the far left, the
coefficient 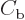 has to be set to zero. The reason was worked
out in chapter 7.10: combinations of exponentials of the
form
has to be set to zero. The reason was worked
out in chapter 7.10: combinations of exponentials of the
form 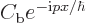 produce wave packets that
propagate backwards in
produce wave packets that
propagate backwards in  , from right to left. Therefore, a
nonzero value for
, from right to left. Therefore, a
nonzero value for  would add an unwanted second wave
packet coming in from the far right.
would add an unwanted second wave
packet coming in from the far right.
Figure A.9:
Example energy eigenfunction for the particle in free space.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
... \put(0,3){\makebox(0,0)[b]{$e^{{\rm i}p x/\hbar}$}}
\end{picture}
\end{figure}](img4974.gif) |
With only the coefficient  of the forward moving part
left, you may as well scale the eigenfunction so that
of the forward moving part
left, you may as well scale the eigenfunction so that 
 1, simplifying it to
1, simplifying it to
A typical example is shown in figure A.9. Plus and minus
the magnitude of the eigenfunction are shown in black, and the real
part is shown in red. This wave function is an eigenfunction of
linear momentum, with 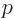 the linear momentum.
the linear momentum.
To produce a coherent wave packet, eigenfunctions with somewhat
different energies  have to be combined together. Since the
momentum is given by
have to be combined together. Since the
momentum is given by 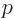

 , different energy
means different momentum
, different energy
means different momentum 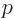 ; therefore the wave packet can be
written as
; therefore the wave packet can be
written as
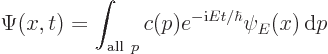 |
(A.206) |
where 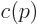 is some function that is only nonzero in a relatively
narrow range of momenta
is some function that is only nonzero in a relatively
narrow range of momenta 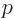 around the nominal momentum. Except for
that basic requirement, the choice of the function
around the nominal momentum. Except for
that basic requirement, the choice of the function 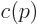 is quite
arbitrary. Choose some suitable function
is quite
arbitrary. Choose some suitable function 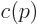 , then use a
computer to numerically integrate the above integral at a large number
of plot points and times. Dump the results into your favorite
animation software and bingo, out comes the movie.
, then use a
computer to numerically integrate the above integral at a large number
of plot points and times. Dump the results into your favorite
animation software and bingo, out comes the movie.
Figure A.10:
Example energy eigenfunction for a particle entering a
constant accelerating force field.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
...\line(0,1){35}}
\put(-.1,15.5){\makebox(0,0)[t]{A}}
\end{picture}
\end{figure}](img4979.gif) |
Next consider the animation of chapter 7.11.2, where
the particle accelerates along a downward potential energy ramp
starting from point A. A typical energy eigenfunction is shown in
figure A.10. Since to the left of point A, the potential
energy is still zero, in that region the energy eigenfunction is still
of the form
where 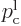 is the momentum that a classical particle
of energy
is the momentum that a classical particle
of energy  would have in the left region. (Quantum mechanics looks
at the complete wave function, not just a single point of it, and
would say that the momentum is uncertain.)
would have in the left region. (Quantum mechanics looks
at the complete wave function, not just a single point of it, and
would say that the momentum is uncertain.)
In this case, it can no longer be argued that the coefficient
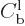 must be zero to avoid a packet entering from the
far right. After all, the
must be zero to avoid a packet entering from the
far right. After all, the
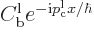 term does
not extend to the far right anymore. To the right of point
term does
not extend to the far right anymore. To the right of point 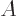 ,
the potential changes linearly with position, and the exponentials are
no longer valid.
,
the potential changes linearly with position, and the exponentials are
no longer valid.
In fact, it is known that the solution of the Hamiltonian eigenvalue
problem in a region with a linearly varying potential is a combination
of two weird functions Ai and Bi that are called the
Airy
functions. The bad news is that if you are
interested in learning more about their properties, you will need an
advanced mathematical handbook like [1] or at
least look at addendum {A.29}. The good news is that
free software to evaluate these functions and their first derivatives
is readily available on the web. The general solution for a linearly
varying potential is of the form
Note that 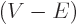

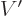 is the
is the  -position measured from the point
where
-position measured from the point
where 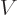

 . Also note that the cube root is negative,
so that
. Also note that the cube root is negative,
so that 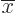 is.
is.
It may be deduced from the approximate analysis of addendum
{A.28} that to prevent a second wave packet coming in from
the far right, Ai and Bi must appear together in the combination
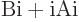 as shown in figure A.10. The fact
that no second packet comes in from the far right in the animation can
be taken as an experimental confirmation of that result, so there
seems little justification to go over the messy argument.
as shown in figure A.10. The fact
that no second packet comes in from the far right in the animation can
be taken as an experimental confirmation of that result, so there
seems little justification to go over the messy argument.
To complete the determination of the eigenfunction for a given value
of  , the constants
, the constants 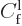 ,
,
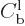 and
and 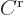 must still be determined. That
goes as follows. For now, assume that
must still be determined. That
goes as follows. For now, assume that 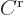 has the
provisional value
has the
provisional value 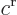
 1. Then provisional values
1. Then provisional values
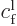 and
and 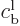 for the other two
constants may be found from the requirements that the left and right
regions give the same values for
for the other two
constants may be found from the requirements that the left and right
regions give the same values for 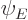 and
and 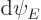

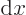 at
the point A in figure A.10 where they meet:
at
the point A in figure A.10 where they meet:
That is equivalent to two equations for the two constants
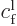 and
and 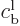 , since
everything else can be evaluated, using the mentioned software. So
, since
everything else can be evaluated, using the mentioned software. So
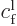 and
and 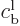 can be found from
solving these two equations.
can be found from
solving these two equations.
As the final step, it is desirable to normalize the eigenfunction
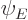 so that
so that 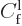
 1. To do so, the entire
provisional eigenfunction can be divided by
1. To do so, the entire
provisional eigenfunction can be divided by
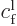 , giving
, giving 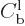

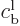

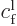 and
and 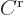

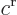

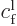 . The energy eigenfunction
has now been found. And since
. The energy eigenfunction
has now been found. And since 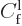
 1, the
1, the
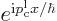 term is exactly the same as the
free space energy eigenfunction of the first example. That means that
if the eigenfunctions
term is exactly the same as the
free space energy eigenfunction of the first example. That means that
if the eigenfunctions 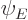 are combined into a wave packet in the
same way as in the free space case, (A.206) with
are combined into a wave packet in the
same way as in the free space case, (A.206) with 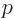 replaced
by
replaced
by 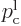 , the
, the
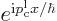 terms produce the exact same
wave packet coming in from the far left as in the free space case.
terms produce the exact same
wave packet coming in from the far left as in the free space case.
For larger times, the
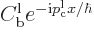 terms
produce a
terms
produce a reflected
wave packet that returns toward
the far left. Note that 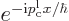 is the
complex conjugate of
is the
complex conjugate of 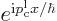 , and
it can be seen from the unsteady Schrödinger equation that if the complex
conjugate of a wave function is taken, it produces a reversal of time.
Wave packets coming in from the far left at large negative times
become wave packets leaving toward the far left at large positive
times. However, the constant
, and
it can be seen from the unsteady Schrödinger equation that if the complex
conjugate of a wave function is taken, it produces a reversal of time.
Wave packets coming in from the far left at large negative times
become wave packets leaving toward the far left at large positive
times. However, the constant 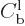 turns out to be
very small in this case, so there is little reflection.
turns out to be
very small in this case, so there is little reflection.
Figure A.11:
Example energy eigenfunction for a particle entering a
constant decelerating force field.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
...\line(0,1){35}}
\put(-.1,15.5){\makebox(0,0)[t]{A}}
\end{picture}
\end{figure}](img4998.gif) |
Next consider the animation of chapter 7.11.3, where the
particle is turned back by an upward potential energy ramp. A typical
energy eigenfunction for this case is shown in figure
A.11. Unlike in the previous example, where the
argument 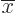 of the Airy functions was negative at the far
right, here it is positive. Table books that cover the Airy functions
will tell you that the Airy function Bi blows up very strongly with
increasing positive argument
of the Airy functions was negative at the far
right, here it is positive. Table books that cover the Airy functions
will tell you that the Airy function Bi blows up very strongly with
increasing positive argument 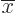 . Therefore, if the
solution in the right hand region would involve any amount of Bi, it
would locate the particle at infinite
. Therefore, if the
solution in the right hand region would involve any amount of Bi, it
would locate the particle at infinite  for all times. For a
particle not at infinity, the solution in the right hand region can
only involve the Airy function Ai. That function decays rapidly with
positive argument
for all times. For a
particle not at infinity, the solution in the right hand region can
only involve the Airy function Ai. That function decays rapidly with
positive argument 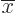 , as seen in figure
A.11.
, as seen in figure
A.11.
The further determination of the energy eigenfunctions proceeds along
the same lines as in the previous example: give 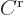 a
provisional value
a
provisional value 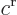
 1, then compute
1, then compute
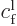 and
and 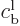 from the requirements
that the left and right regions produce the same values for
from the requirements
that the left and right regions produce the same values for 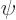 and
and
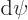

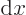 at the point A where they meet. Finally divide the
eigenfunction by
at the point A where they meet. Finally divide the
eigenfunction by 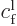 . The big difference is
that now
. The big difference is
that now 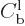 is no longer small;
is no longer small;
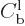 turns out to be of unit magnitude just like
turns out to be of unit magnitude just like
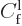 . It means that the incoming wave packet
is reflected back completely.
. It means that the incoming wave packet
is reflected back completely.
Figure A.12:
Example energy eigenfunction for the harmonic
oscillator.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(405,75...
...mex.eps}}}
\put(0,2){\makebox(0,0)[b]{$h_{50}(x)$}}
\end{picture}
\end{figure}](img5000.gif) |
For the harmonic oscillator of chapter 7.11.4, the
analysis is somewhat different. In particular, chapter
4.1.2 showed that the energy levels of the one-dimensional
harmonic oscillator are discrete,
so that unlike the motions just discussed, the solution of the
Schrödinger equation is a sum, rather than the integral
(A.206),
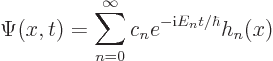
However, for large  the difference between summation and
integration is small.
the difference between summation and
integration is small.
Also, while the energy eigenfunctions 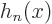 are not exponentials as
for the free particle, for large
are not exponentials as
for the free particle, for large  they can be pairwise combined to
approximate such exponentials. For example, eigenfunction
they can be pairwise combined to
approximate such exponentials. For example, eigenfunction
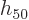 , shown in figure A.12, behaves near the
center point much like a cosine if you scale it properly. Similarly,
, shown in figure A.12, behaves near the
center point much like a cosine if you scale it properly. Similarly,
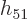 behaves much like a sine. A cosine plus
behaves much like a sine. A cosine plus 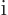 times a sine
gives an exponential, according to the Euler formula (2.5).
Create similar exponential combinations of eigenfunctions with even
and odd values of
times a sine
gives an exponential, according to the Euler formula (2.5).
Create similar exponential combinations of eigenfunctions with even
and odd values of  for a range of
for a range of  values, and there are the
approximate exponentials that allow you to create a wave packet that
is at the center point at time
values, and there are the
approximate exponentials that allow you to create a wave packet that
is at the center point at time 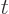
 0. In the animation, the
range of
0. In the animation, the
range of  values was centered around
values was centered around 
 50, making the
nominal energy hundred times the ground state energy. The
exponentials degenerate over time, since their component
eigenfunctions have slightly different energy, hence time evolution.
That explains why after some time, the wave packet can return to the
center point going the other way.
50, making the
nominal energy hundred times the ground state energy. The
exponentials degenerate over time, since their component
eigenfunctions have slightly different energy, hence time evolution.
That explains why after some time, the wave packet can return to the
center point going the other way.
Figure A.13:
Example energy eigenfunction for a particle encountering a
brief accelerating force.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
....5){\line(0,-1){3}}
\put(8,20){\makebox(0,0)[b]{B}}
\end{picture}
\end{figure}](img5006.gif) |
For the particle of chapter 7.12.1 that encounters a brief
accelerating force, an example eigenfunction looks like figure
A.13. In this case, the solution in the far right region
is similar to the one in the far left region. However, there cannot
be a term of the form 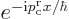 in the
far right region, because when the eigenfunctions are combined, it
would produce an unwanted wave packet coming in from the far right.
In the middle region of linearly varying potential, the wave function
is again a combination of the two Airy functions. The way to find the
constants now has an additional step. First give the constant
in the
far right region, because when the eigenfunctions are combined, it
would produce an unwanted wave packet coming in from the far right.
In the middle region of linearly varying potential, the wave function
is again a combination of the two Airy functions. The way to find the
constants now has an additional step. First give the constant
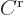 of the far right exponential the provisional value
of the far right exponential the provisional value
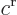
 1 and from that, compute provisional values
1 and from that, compute provisional values
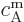 and
and 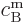 by demanding that the
Airy functions give the same values for
by demanding that the
Airy functions give the same values for 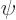 and
and 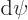

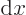 as
the far-right exponential at point B, where they meet. Next compute
provisional values
as
the far-right exponential at point B, where they meet. Next compute
provisional values 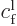 and
and 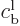 by
demanding that the far-left exponentials give the same values for
by
demanding that the far-left exponentials give the same values for
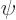 and
and 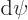

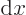 as the Airy functions at point A, where
they meet. Finally, divide all the constants by
as the Airy functions at point A, where
they meet. Finally, divide all the constants by 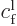 to make
to make 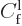
 1.
1.
Figure A.14:
Example energy eigenfunction for tunneling through a
barrier.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,54...
...15){\line(0,-1){3}}
\put(8,20){\makebox(0,0)[b]{B}}
\end{picture}
\end{figure}](img5010.gif) |
For the tunneling particle of chapter 7.12.2, an example
eigenfunction is as shown in figure A.14. In this case,
the solution in the middle part is not a combination of Airy
functions, but of real exponentials. It is essentially the same
solution as in the left and right parts, but in the middle region the
potential energy is greater than the total energy, making
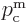

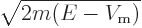 an imaginary
number. Therefore the arguments of the exponentials become real when
written in terms of the absolute value of the momentum
an imaginary
number. Therefore the arguments of the exponentials become real when
written in terms of the absolute value of the momentum
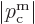

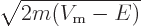 . The
rest of the analysis is similar to that of the previous example.
. The
rest of the analysis is similar to that of the previous example.
Figure A.15:
Tunneling through a delta function barrier.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
...\line(0,1){35}}
\put(-.1,15.5){\makebox(0,0)[t]{A}}
\end{picture}
\end{figure}](img5015.gif) |
For the particle tunneling through the delta function potential in
chapter 7.12.2, an example energy eigenfunction is shown
in figure A.15. The potential energy in this case is 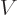

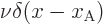 , where
, where 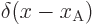 is
a spike at point A that integrates to one and the strength
is
a spike at point A that integrates to one and the strength 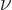 is a
chosen constant. In the example,
is a
chosen constant. In the example, 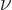 was chosen to be
was chosen to be
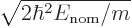 with
with  the nominal
energy. For that strength, half the wave packet will pass through.
the nominal
energy. For that strength, half the wave packet will pass through.
For a delta function potential, a modification must be made in the
analysis as used so far. As figure A.15 illustrates, there
are kinks in the energy eigenfunction at the location A of the delta
function. The left and right expressions for the eigenfunction
do not predict the same value for its derivative
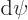

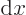 at point A. To find the difference, integrate
the Hamiltonian eigenvalue problem from a point a very short distance
at point A. To find the difference, integrate
the Hamiltonian eigenvalue problem from a point a very short distance
 before point A to a point the same very short distance
behind it:
before point A to a point the same very short distance
behind it:
The integral in the right hand side is zero because of the vanishingly
small interval of integration. But the delta function spike in the
left hand side integrates to one regardless of the small integration
range, so
For vanishingly small  ,
, 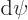

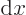 at
at
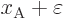 becomes what the right hand part of the
eigenfunction gives for
becomes what the right hand part of the
eigenfunction gives for 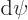

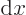 at
at 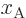 ,
while
,
while 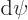

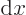 at
at 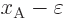 becomes what the
left hand part gives for it. As seen from the above equation, the
difference is not zero, but
becomes what the
left hand part gives for it. As seen from the above equation, the
difference is not zero, but 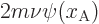

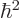 .
.
So the correct equations for the provisional constants are in this case
Compared to the analysis as used previously, the difference is the
final term in the second equation that is added by the delta function.
The remainder of this note gives some technical details for if you are
actually planning to do your own animations. It is a good idea to
assume that the units of mass, length, and time are chosen such that
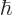 and the nominal energy are one, while the mass of the particle
is one-half. That avoids having to guesstimate suitable values for
all sorts of very small numbers. The Hamiltonian eigenvalue problem
then simplifies to
and the nominal energy are one, while the mass of the particle
is one-half. That avoids having to guesstimate suitable values for
all sorts of very small numbers. The Hamiltonian eigenvalue problem
then simplifies to
where the values of  of interest cluster around 1. The nominal
momentum will be one too. In those units, the length of the plotted
range was one hundred in all but the harmonic oscillator case.
of interest cluster around 1. The nominal
momentum will be one too. In those units, the length of the plotted
range was one hundred in all but the harmonic oscillator case.
It should be noted that to select a good function 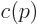 in
(A.206) is somewhat of an art. The simplest idea would be to
choose
in
(A.206) is somewhat of an art. The simplest idea would be to
choose 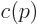 equal to one in some limited range around the nominal
momentum, and zero elsewhere, as in
equal to one in some limited range around the nominal
momentum, and zero elsewhere, as in
where 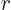 is the relative deviation from the nominal momentum below
which
is the relative deviation from the nominal momentum below
which 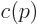 is nonzero. However, it is know from Fourier analysis
that the locations where
is nonzero. However, it is know from Fourier analysis
that the locations where 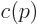 jumps from one to zero lead to lengthy
wave packets when viewed in physical space.
{D.44}. Functions
jumps from one to zero lead to lengthy
wave packets when viewed in physical space.
{D.44}. Functions 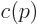 that do lead to nice compact wave
packets are known to be of the form
that do lead to nice compact wave
packets are known to be of the form
And that is essentially the function 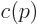 used in this study. The
typical width of the momentum range was chosen to be
used in this study. The
typical width of the momentum range was chosen to be 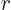
 0.15, or
15%, by trial and error. However, it is nice if
0.15, or
15%, by trial and error. However, it is nice if 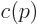 becomes not
just very small, but exactly zero beyond some point, for one because
it cuts down on the number of energy eigenfunctions that have to be
evaluated numerically. Also, it is nice not to have to worry about
the possibility of
becomes not
just very small, but exactly zero beyond some point, for one because
it cuts down on the number of energy eigenfunctions that have to be
evaluated numerically. Also, it is nice not to have to worry about
the possibility of 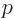 being negative in writing energy
eigenfunctions. Therefore, the final function used was
being negative in writing energy
eigenfunctions. Therefore, the final function used was
The actual difference in numerical values is small, but it does make
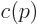 exactly zero for negative momenta and those greater than twice
the nominal value. Strictly speaking,
exactly zero for negative momenta and those greater than twice
the nominal value. Strictly speaking, 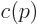 should still be
multiplied by a constant to make the total probability of finding the
particle equal to one. But if you do not tell people what numbers for
should still be
multiplied by a constant to make the total probability of finding the
particle equal to one. But if you do not tell people what numbers for
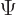 are on the vertical axes, you do not need to bother.
are on the vertical axes, you do not need to bother.
In doing the numerical integrations to find 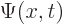 , note
that the mid point and trapezium rules of numerical integration are
exponentially accurate under the given conditions, so there is
probably not much motivation to try more advanced methods. The mid
point rule was used.
, note
that the mid point and trapezium rules of numerical integration are
exponentially accurate under the given conditions, so there is
probably not much motivation to try more advanced methods. The mid
point rule was used.
The animations in this book used the numerical implementations daie.f, dbie.f, daide.f, and dbide.f from netlib.org for the
Airy functions and their first derivatives. These offer some basic
protection against underflow and overflow by splitting off an
exponential for positive  . It may be a good idea
to check for underflow and overflow in general and use 64 bit
precision. The examples here did.
. It may be a good idea
to check for underflow and overflow in general and use 64 bit
precision. The examples here did.
For the harmonic oscillator, the larger the nominal energy is compared
to the ground state energy, the more the wave packet can resemble a
single point compared to the limits of motion. However, the computer
program used to create the animation computed the eigenfunctions by
evaluating the analytical expression given in derivation
{D.12}, and explicitly evaluating the Hermite
polynomials is very round-off sensitive. That limited it to a maximum
of about hundred times the ground state energy when allowing for
enough uncertainty to localize the wave packet. Round-off is a
general problem for power series, not just for the Hermite
polynomials. If you want to go to higher energies to get a smaller
wave packet, you will want to use a finite difference or finite
element method to find the eigenfunctions.
The plotting software used to produce the animations was a mixture of
different programs. There are no doubt much simpler and better ways
of doing it. In the animations presented here, first plots were
created of 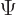 versus
versus  for a large number of closely spaced
times covering the duration of the animation. These plots were
converted to gifs using a mixture of personal software, netpbm, and
ghostview. The gifs were then combined into a single movie using
gifsicle.
for a large number of closely spaced
times covering the duration of the animation. These plots were
converted to gifs using a mixture of personal software, netpbm, and
ghostview. The gifs were then combined into a single movie using
gifsicle.
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ;
;![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
...\line(0,1){35}}
\put(-.1,15.5){\makebox(0,0)[t]{A}}
\end{picture}
\end{figure}](img4979.gif)
![]()
![]()
![]() ,
,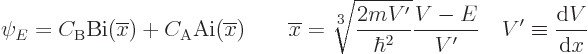
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\begin{eqnarray*}
& \displaystyle
c^{\rm {l}}_{\rm {f}}e^{{\rm i}p_{\rm {c}}^{...
...rline{x}_{\rm {A}})\right]
\frac{{\rm d}\overline{x}}{{\rm d}x}
\end{eqnarray*}](img4995.gif)
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
...\line(0,1){35}}
\put(-.1,15.5){\makebox(0,0)[t]{A}}
\end{picture}
\end{figure}](img4998.gif)
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.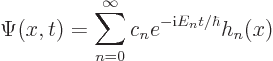
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,53...
....5){\line(0,-1){3}}
\put(8,20){\makebox(0,0)[b]{B}}
\end{picture}
\end{figure}](img5006.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
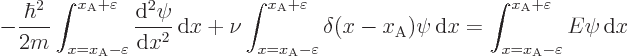
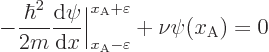
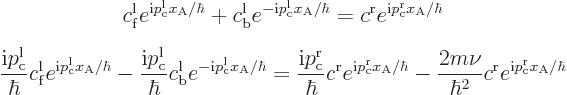
![]()
![]()
![]()
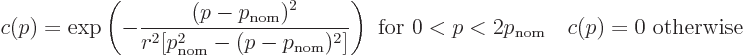
![]() ,
,![]() .
.![]()
![]()